题目内容
在三角形ABC中，a、b、c是角A、B、C的对边，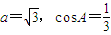
，则
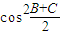= ；b2+c2的最大值是 ．
【答案】分析：先根据A+B+C=180°知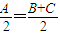
，进而可知
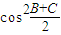=sin2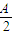
，再利用二倍角公式求得sin2
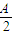，即可得到答案．
由余弦定理关于b，c的关系式得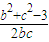
=
再根据b2+c2≥2bc进而求得b2+c2的范围．
解答：解：∵A+B+C=180°
∴B+C=180°-A，∴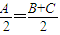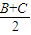
∴cos2
=cos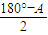2
=sin2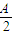
=
=
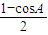由余弦定理可知cosA=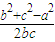
∴
=
，∴
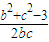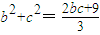
∵b2+c2≥2bc，
∴
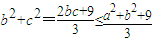
∴b2+c2≤
故答案为：
，
点评：本题主要考查正弦定理和余弦定理在解三角形中的应用．属基础题．
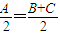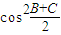，进而可知=sin2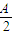，再利用二倍角公式求得sin2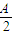，即可得到答案．由余弦定理关于b，c的关系式得
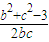=再根据b2+c2≥2bc进而求得b2+c2的范围．解答：解：∵A+B+C=180°
∴B+C=180°-A，∴
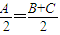
∴cos2
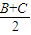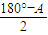=cos2=sin2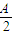==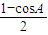由余弦定理可知cosA=
∴
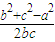
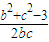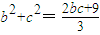
=，∴∵b2+c2≥2bc，
∴
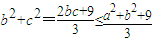
∴b2+c2≤
故答案为：
，点评：本题主要考查正弦定理和余弦定理在解三角形中的应用．属基础题．
练习册系列答案
相关题目