题目内容
(2014•兰州一模)已知函数f(x)=lnx,g(x)=f(x)+ax2+bx,函数g(x)的图象在点(1,g(1))处的切线平行于x轴.
(1)确定a与b的关系;
(2)若a≥0,试讨论函数g(x)的单调性;
(3)设斜率为k的直线与函数f(x)的图象交于两点A(x1,y1),B(x2,y2),(x1<x2)
证明:
<k<
.
(1)确定a与b的关系;
(2)若a≥0,试讨论函数g(x)的单调性;
(3)设斜率为k的直线与函数f(x)的图象交于两点A(x1,y1),B(x2,y2),(x1<x2)
证明:
| 1 |
| x2 |
| 1 |
| x1 |
分析:(1)利用导数的几何意义即可得出;
(2)通过求导得到g′(x),通过对a分类讨论即可得出其单调性;
(3)证法一:利用斜率计算公式,令
=t(t>1),即证1-
<lnt<t-1(t>1),令h(t)=lnt+
-1(t>1),通过求导利用函数的单调性即可得出;
证法二:利用斜率计算公式,令h(x)=lnx-kx,通过求导,利用导数研究其单调性即可得出;
证法三::令h(x)=lnx-
,同理,令m(x)=lnx-
,通过求导即可证明;
证法四:利用斜率计算公式,令h(x)=x-x1lnx+x1lnx1-x1,及令m(x)=x-x2lnx+x2lnx2-x2,通过求导得到其单调性即可证明.
(2)通过求导得到g′(x),通过对a分类讨论即可得出其单调性;
(3)证法一:利用斜率计算公式,令
| x2 |
| x1 |
| 1 |
| t |
| 1 |
| t |
证法二:利用斜率计算公式,令h(x)=lnx-kx,通过求导,利用导数研究其单调性即可得出;
证法三::令h(x)=lnx-
| x |
| x1 |
| x |
| x2 |
证法四:利用斜率计算公式,令h(x)=x-x1lnx+x1lnx1-x1,及令m(x)=x-x2lnx+x2lnx2-x2,通过求导得到其单调性即可证明.
解答:解:(1)依题意得g(x)=lnx+ax2+bx,则g′(x)=
+2ax+b,
由函数g(x)的图象在点(1,g(1))处的切线平行于x轴得:g'(1)=1+2a+b=0,
∴b=-2a-1.
(2)由(1)得g′(x)=
=
.
∵函数g(x)的定义域为(0,+∞),∴当a=0时,g′(x)=-
,
由g'(x)>0得0<x<1,由g'(x)<0得x>1,
即函数g(x)在(0,1)上单调递增,在(1,+∞)单调递减;
当a>0时,令g'(x)=0得x=1或x=
,
若
<1,即a>
时,由g'(x)>0得x>1或0<x<
,由g'(x)<0得
<x<1,
即函数g(x)在(0,
),(1,+∞)上单调递增,在(
,1)单调递减;
若
>1,即0<a<
时,由g'(x)>0得x>
或0<x<1,由g'(x)<0得1<x<
,
即函数g(x)在(0,1),(
,+∞)上单调递增,在(1,
)单调递减;
若
=1,即a=
时,在(0,+∞)上恒有g'(x)≥0,
即函数g(x)在(0,+∞)上单调递增,
综上得:当a=0时,函数g(x)在(0,1)上单调递增,在(1,+∞)单调递减;
当0<a<
时,函数g(x)在(0,1)单调递增,在(1,
)单调递减;在(
,+∞)上单调递增;
当a=
时,函数g(x)在(0,+∞)上单调递增,
当a>
时,函数g(x)在(0,
)上单调递增,在(
,1)单调递减;在(1,+∞)上单调递增.
(3)证法一:依题意得k=
=
,
证
<k<
,即证
<
<
,因x2-x1>0,即证
<ln
<
,
令
=t(t>1),即证1-
<lnt<t-1(t>1),
令h(t)=lnt+
-1(t>1),则h′(t)=
-
=
>0,∴h(t)在(1,+∞)上单调递增,
∴h(t)>h(1)=0,即lnt>1-
(t>1)②
综合①②得1-
<lnt<t-1(t>1),即
<k<
.
证法二:依题意得k=
=
⇒lnx2-kx2=lnx1-kx1,
令h(x)=lnx-kx,则h′(x)=
-k,
由h'(x)=0得x=
,当x>
时,h'(x)<0,当0<x<
时,h'(x)>0,
∴h(x)在(0,
)单调递增,在(
,+∞)单调递减,又h(x1)=h(x2),
∴x1<
<x2,即
<k<
.
证法三:令h(x)=lnx-
,则h′(x)=
-
,
当x>x1时,h'(x)<0,∴函数h(x)在(x1,+∞)单调递减,
∴当x2>x1时,h(x2)<h(x1)⇒lnx2-
<lnx1-1,即
<
;
同理,令m(x)=lnx-
,可证得
<
.
证法四:依题意得k=
=
,
<k<
?
<
<
?x1lnx2-x1lnx1<x2-x1<x2lnx2-x2lnx1
令h(x)=x-x1lnx+x1lnx1-x1,则h′(x)=1-
,当x>x1时,h'(x)>0,∴函数h(x)在(x1,+∞)单调递增,
∴当x2>x1时,h(x2)>h(x1)=0,即x1lnx2-x1lnx1<x2-x1
令m(x)=x-x2lnx+x2lnx2-x2,则m′(x)=1-
,当x<x2时,m'(x)<0,∴函数m(x)在(0,x2)单调递减,
∴当x1<x2时,m(x1)>h(x2)=0,即x2-x1<x2lnx2-x2lnx1;
所以命题得证.
| 1 |
| x |
由函数g(x)的图象在点(1,g(1))处的切线平行于x轴得:g'(1)=1+2a+b=0,
∴b=-2a-1.
(2)由(1)得g′(x)=
| 2ax2-(2a+1)x+1 |
| x |
| (2ax-1)(x-1) |
| x |
∵函数g(x)的定义域为(0,+∞),∴当a=0时,g′(x)=-
| x-1 |
| x |
由g'(x)>0得0<x<1,由g'(x)<0得x>1,
即函数g(x)在(0,1)上单调递增,在(1,+∞)单调递减;
当a>0时,令g'(x)=0得x=1或x=
| 1 |
| 2a |
若
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2a |
即函数g(x)在(0,
| 1 |
| 2a |
| 1 |
| 2a |
若
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2a |
即函数g(x)在(0,1),(
| 1 |
| 2a |
| 1 |
| 2a |
若
| 1 |
| 2a |
| 1 |
| 2 |
即函数g(x)在(0,+∞)上单调递增,
综上得:当a=0时,函数g(x)在(0,1)上单调递增,在(1,+∞)单调递减;
当0<a<
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2a |
当a=
| 1 |
| 2 |
当a>
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2a |
(3)证法一:依题意得k=
| y2-y1 |
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
证
| 1 |
| x2 |
| 1 |
| x1 |
| 1 |
| x2 |
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| x1 |
| x2-x1 |
| x2 |
| x2 |
| x1 |
| x2-x1 |
| x1 |
令
| x2 |
| x1 |
| 1 |
| t |
令h(t)=lnt+
| 1 |
| t |
| 1 |
| t |
| 1 |
| t2 |
| t-1 |
| t2 |
∴h(t)>h(1)=0,即lnt>1-
| 1 |
| t |
综合①②得1-
| 1 |
| t |
| 1 |
| x2 |
| 1 |
| x1 |
证法二:依题意得k=
| y2-y1 |
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
令h(x)=lnx-kx,则h′(x)=
| 1 |
| x |
由h'(x)=0得x=
| 1 |
| k |
| 1 |
| k |
| 1 |
| k |
∴h(x)在(0,
| 1 |
| k |
| 1 |
| k |
∴x1<
| 1 |
| k |
| 1 |
| x2 |
| 1 |
| x1 |
证法三:令h(x)=lnx-
| x |
| x1 |
| 1 |
| x |
| 1 |
| x1 |
当x>x1时,h'(x)<0,∴函数h(x)在(x1,+∞)单调递减,
∴当x2>x1时,h(x2)<h(x1)⇒lnx2-
| x2 |
| x1 |
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| x1 |
同理,令m(x)=lnx-
| x |
| x2 |
| 1 |
| x2 |
| lnx2-lnx1 |
| x2-x1 |
证法四:依题意得k=
| y2-y1 |
| x2-x1 |
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| x2 |
| 1 |
| x1 |
| 1 |
| x2 |
| lnx2-lnx1 |
| x2-x1 |
| 1 |
| x1 |
令h(x)=x-x1lnx+x1lnx1-x1,则h′(x)=1-
| x1 |
| x |
∴当x2>x1时,h(x2)>h(x1)=0,即x1lnx2-x1lnx1<x2-x1
令m(x)=x-x2lnx+x2lnx2-x2,则m′(x)=1-
| x2 |
| x |
∴当x1<x2时,m(x1)>h(x2)=0,即x2-x1<x2lnx2-x2lnx1;
所以命题得证.
点评:熟练掌握利用导数研究函数的单调性、导数的几何意义、分类讨论思想方法、根据所证明的结论恰当的构造函数、一题多解等是解题的关键.

练习册系列答案
相关题目
 (2014•兰州一模)【选修4-1:几何证明选讲】
(2014•兰州一模)【选修4-1:几何证明选讲】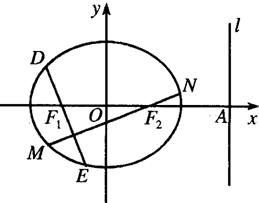 (2014•兰州一模)设椭圆
(2014•兰州一模)设椭圆