题目内容
已知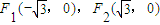 ,点P满足
,点P满足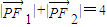 ,记点P的轨迹为E,
,记点P的轨迹为E,(1)求轨迹E的方程;
(2)如果过点Q(0,m)且方向向量为
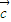 =(1,1)的直线l与点P的轨迹交于A,B两点,当
=(1,1)的直线l与点P的轨迹交于A,B两点,当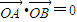 时,求△AOB的面积.
时,求△AOB的面积.
【答案】分析:解:(1)点P满足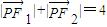 ,得出点P的轨迹是以(
,得出点P的轨迹是以(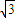 ,0),(-
,0),(-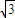 ,0)为焦点的椭圆从而写出点P的轨迹方程即可.
,0)为焦点的椭圆从而写出点P的轨迹方程即可.
(2)依题意直线AB的方程为y=x+m,设A(x1,y1),B(x2,y2)代入椭圆方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量垂直的条件可求得m值,最后利用弦长公式结合三角形的面积公式即可解决问题.
解答:解:(1)∵点P满足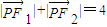 ,
,
∴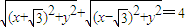
∴点P的轨迹是以(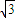 ,0),(-
,0),(-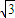 ,0)为焦点的椭圆,
,0)为焦点的椭圆,
a=2,c=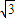 ,b=1,
,b=1,
∴点P的轨迹方程为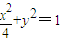
(2)依题意直线AB的方程为y=x+m.
设A(x1,y1),B(x2,y2)
代入椭圆方程,得5x2+8mx+4m2-4=0,(1分)△=64m2-20(4m2-4)>0,∴m2<5,
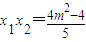 ,
,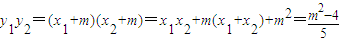 ,
,
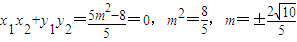 ,
,
因此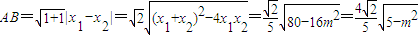 =
=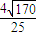 ,
,
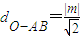 =
=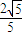 ,
,
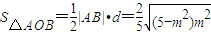 =
=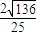 .
.
点评:本题考查椭圆的性质与其性质的应用,注意(2)的处理弦长问题的一般方法,将直线的方程代入椭圆方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得m值,从而解决问题.
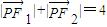 ,得出点P的轨迹是以(
,得出点P的轨迹是以(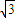 ,0),(-
,0),(-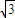 ,0)为焦点的椭圆从而写出点P的轨迹方程即可.
,0)为焦点的椭圆从而写出点P的轨迹方程即可.(2)依题意直线AB的方程为y=x+m,设A(x1,y1),B(x2,y2)代入椭圆方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量垂直的条件可求得m值,最后利用弦长公式结合三角形的面积公式即可解决问题.
解答:解:(1)∵点P满足
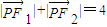 ,
,∴
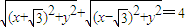
∴点P的轨迹是以(
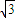 ,0),(-
,0),(-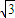 ,0)为焦点的椭圆,
,0)为焦点的椭圆,a=2,c=
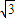 ,b=1,
,b=1,∴点P的轨迹方程为
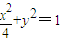
(2)依题意直线AB的方程为y=x+m.
设A(x1,y1),B(x2,y2)
代入椭圆方程,得5x2+8mx+4m2-4=0,(1分)△=64m2-20(4m2-4)>0,∴m2<5,
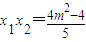 ,
,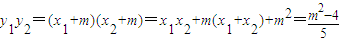 ,
,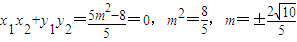 ,
,因此
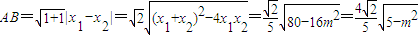 =
=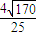 ,
,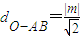 =
=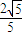 ,
,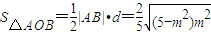 =
=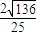 .
.点评:本题考查椭圆的性质与其性质的应用,注意(2)的处理弦长问题的一般方法,将直线的方程代入椭圆方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得m值,从而解决问题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
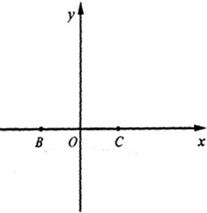 已知点B(-1,0)、C(1,0),平面上的动点P满足
已知点B(-1,0)、C(1,0),平面上的动点P满足 中,已知三点
中,已知三点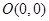 ,
,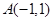 ,
,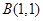 ,曲线C上任意—点
,曲线C上任意—点 满足:
满足: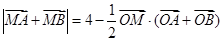 .
.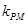 ,
,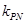 .试探究
.试探究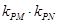 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论;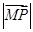 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.