题目内容
(本小题满分12分)
在平面直角坐标系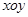 中,已知三点
中,已知三点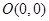 ,
,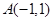 ,
,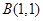 ,曲线C上任意—点
,曲线C上任意—点 满足:
满足: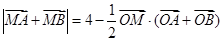 .
.
(l)求曲线C的方程;
(2)设点P是曲线C上的任意一点,过原点的直线L与曲线相交于M,N两点,若直线PM,PN的斜率都存在,并记为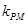 ,
,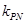 .试探究
.试探究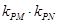 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论;
(3)设曲线C与y轴交于D、E两点,点M (0,m)在线段DE上,点P在曲线C上运动.若当点P的坐标为(0,2)时,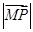 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.
【答案】
(l) 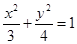 (2)
(2) 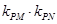
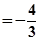 (3)
(3) 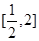
【解析】
试题分析:(1)由题意可得,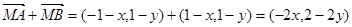 ,
,
所以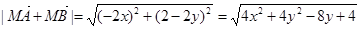 ,
,
又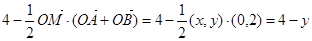 ,
,
所以 ,即
,即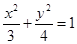 .
.
(2)因为过原点的直线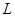 与椭圆相交的两点
与椭圆相交的两点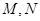 关于坐标原点对称,
关于坐标原点对称,
所以可设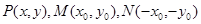 .
.
因为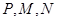 在椭圆上,所以有
在椭圆上,所以有
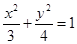 , ………①
, ………①
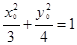 , ………②
, ………②
①-②得
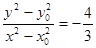 .
.
又 ,
,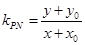 ,
,
所以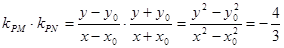 ,
,
故 的值与点
的值与点 的位置无关,与直线
的位置无关,与直线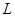 也无关.
也无关.
(3)由于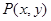 在椭圆
在椭圆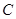 上运动,椭圆方程为
上运动,椭圆方程为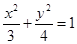 ,故
,故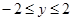 ,且
,且
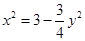 . 因为
. 因为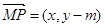 ,所以
,所以
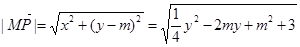
 .
.
由题意,点 的坐标为
的坐标为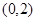 时,
时,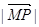 取得最小值,即当
取得最小值,即当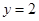 时,
时,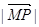 取得最
取得最
小值,而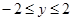 ,故有
,故有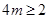 ,解得
,解得 .
.
又椭圆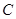 与
与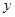 轴交于
轴交于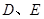 两点的坐标为
两点的坐标为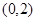 、
、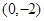 ,而点
,而点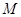 在线段
在线段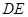 上, 即
上, 即 ,亦即
,亦即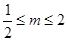 ,所以实数
,所以实数 的取值范围是
的取值范围是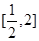 .
.
考点:求动点的轨迹方程及椭圆与直线相交的性质
点评:求轨迹方程的大体步骤:1建立直角坐标系,设出动点坐标,2找到关于动点的关系式,3关系式坐标化,整理化简,4除去不满足题意要求的个别点。本题第二三小题较复杂,学生很难达到满分

练习册系列答案
相关题目