题目内容
15. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<0).(1)若f(x)的部分图象如图所示,求f(x)的解折式;
(2)在(1)的条件下,求最小正实数m,使得函数f(x)的图象向左平移m个单位后所对应的函数是偶函数;
(3)若f(x)在[0,$\frac{π}{3}$]上是单调递增函数,求ω最大值.
分析 (1)根据函数图象确定A,ω和φ的值即可.
(2)根据三角函数平移关系,结合偶函数的性质即可得到结论.
(3)根据三角函数单调性和周期之间的关系建立不等式关系即可.
解答 解:(1)由图象知A=2,
函数的周期T=4•($\frac{π}{3}$-$\frac{π}{12}$)=4×$\frac{3π}{12}$=π,
即$\frac{2π}{ω}$=π,则ω=2,
即f(x)=2sin(2x+φ),
由f($\frac{π}{3}$)=2sin(2×$\frac{π}{3}$+φ)=2,
即sin($\frac{2π}{3}$+φ)=1,
则$\frac{2π}{3}$+φ=$\frac{π}{2}$+2kπ,k∈Z,
则φ=-$\frac{π}{6}$+2kπ,k∈Z,
∵-π<φ<0,
∴当k=0时,φ=-$\frac{π}{6}$,
此时f(0)=2sinφ=-1成立,
即f(x)=2sin(2x-$\frac{π}{6}$).
(2)若f(x)=2sin(2x-$\frac{π}{6}$)的图象向左平移m个单位,得到y=2sin[2(x+m)-$\frac{π}{6}$]=2sin(2x+2m-$\frac{π}{6}$),
若此时函数为偶函数,
则2m-$\frac{π}{6}$=$\frac{π}{2}$+kπ,即m=$\frac{π}{3}$+$\frac{kπ}{2}$,k∈Z,
∴当k=0时,m为最小的正实数此时m=$\frac{π}{3}$.
(3)若f(x)在[0,$\frac{π}{3}$]上是单调递增函数,
则$\frac{T}{2}$≥$\frac{π}{3}$,即T≥$\frac{2π}{3}$,
即$\frac{2π}{ω}$≥$\frac{2π}{3}$,
∴ω≤3,即ω最大值为3.
点评 本题主要考查三角函数解析式的求解以及三角函数单调性的应用,考查学生的运算和推理能力.


| A. | 5 | B. | 3 | C. | -5 | D. | -3 |
| A. | $\frac{a+b}{2}$ | B. | $\frac{a-b}{2}$ | C. | $\frac{a+b}{a-b}$ | D. | $\frac{a-b}{a+b}$ |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{3}$ |
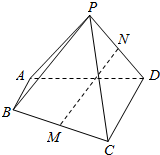 如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点.
如图,四棱锥P-ABCD中,AB∥CD,AB⊥AD,BC=CD=2AB=2,△PAD是等边三角形,M、N分别为BC、PD的中点. 如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上的一点.
如图所示,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上的一点.