题目内容
过点M（3，0）作直线l与圆x2+y2=25交于A、B两点．（1）若点P是线段AB的中点，求点P的轨迹方程；
（2）求直线l的倾斜角为何值时△AOB的面积最大，并求这个最大值．
【答案】分析：（1）设出G的坐标，利用Rt△OMP中必有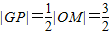
．说明P点的轨迹为以G为圆心
为半径的圆，得到P的轨迹方程．
（2）令|OP|=h，由题意知0＜h≤3，求出△AOB的面积的表达式，利用二次函数在闭区间上的最大值求解即可．
解答：解：（1）∵P是AB中点，∴OP⊥AB，取OM中点G，则在Rt△OMP中必有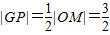
．
∴P点的轨迹为以G为圆心
为半径的圆，令P（x，y）则
，
即x2-3x+y2=0．
经检验知：AB为x轴及AB∥y轴均满足上式，∴P点的轨迹为x2-3x+y2=0…（6分）
（2）令|OP|=h，由题意知0＜h≤3，
在Rt△APO中，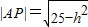
即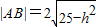
，
=
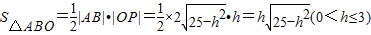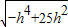（0＜h≤3）．
令t=h2则 0＜t≤9，
易知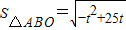
，在 0＜t≤9时单调递增．
∴当t=9，即直线AB垂直x轴时，S△ABOmax=12，此时l的倾斜角为90°．
点评：本题是综合题，考查曲线轨迹方程的求法，转化思想的应用，二次函数闭区间最值的求法，考查计算能力．
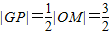．说明P点的轨迹为以G为圆心为半径的圆，得到P的轨迹方程．（2）令|OP|=h，由题意知0＜h≤3，求出△AOB的面积的表达式，利用二次函数在闭区间上的最大值求解即可．
解答：解：（1）∵P是AB中点，∴OP⊥AB，取OM中点G，则在Rt△OMP中必有
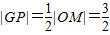．∴P点的轨迹为以G为圆心
为半径的圆，令P（x，y）则，即x2-3x+y2=0．
经检验知：AB为x轴及AB∥y轴均满足上式，∴P点的轨迹为x2-3x+y2=0…（6分）
（2）令|OP|=h，由题意知0＜h≤3，
在Rt△APO中，
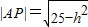即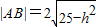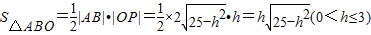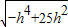，=（0＜h≤3）．令t=h2则 0＜t≤9，
易知
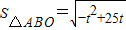，在 0＜t≤9时单调递增．∴当t=9，即直线AB垂直x轴时，S△ABOmax=12，此时l的倾斜角为90°．
点评：本题是综合题，考查曲线轨迹方程的求法，转化思想的应用，二次函数闭区间最值的求法，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．