题目内容
已知椭圆C: +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).(1)求椭圆的方程;
(2)若直MA交直x=4于点P,过P作直线MB的垂线x轴于点Q,Q的坐标;
(3)求点P在直线MB上射R的轨迹方程.
【答案】分析:(1)先确定双曲线中c的值,再利用椭圆的离心率,即可确定椭圆的方程;
(2)设M(x,y),P(4,z),则可得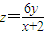 ,利用PQ⊥MB及M在椭圆上,即可求Q的坐标;
,利用PQ⊥MB及M在椭圆上,即可求Q的坐标;
(3)点P在直线MB上射影即PQ与MB的交点H,由QH⊥HB得△HQB为直角三角形,从而可求H点的轨迹方程.
解答: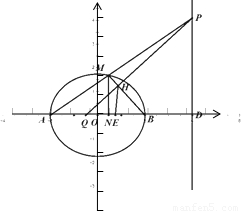 解:(1)由题意知,双曲线4x2-
解:(1)由题意知,双曲线4x2- y2=1,∴c=1,
y2=1,∴c=1,
∵椭圆的离心率为e= ,∴a=2,
,∴a=2,
∴b2=a2-c2=3
∴椭圆方程为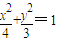 (3分)
(3分)
(2)设M(x,y),P(4,z),则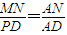 ,得
,得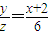 ,故
,故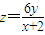 .
.
设Q(x,0),由PQ⊥MB得: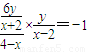 ,
,
又M在椭圆上,故x2=4-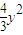 ,化简得
,化简得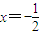 ,即Q(
,即Q(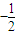 ,0)(8分)
,0)(8分)
(3)点P在直线MB上射影即PQ与MB的交点H,由QH⊥HB得△HQB为直角三角形,
设E为QB中点,则|HE|= |QB|=
|QB|= ,E(
,E( ,0),
,0),
因此H点的轨迹方程为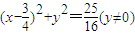 (13分)
(13分)
点评:本题考查椭圆的标准方程,考查轨迹方程,解题的关键是确定椭圆中的几何量,利用垂直关系,建立等式,属于中档题.
(2)设M(x,y),P(4,z),则可得
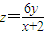 ,利用PQ⊥MB及M在椭圆上,即可求Q的坐标;
,利用PQ⊥MB及M在椭圆上,即可求Q的坐标;(3)点P在直线MB上射影即PQ与MB的交点H,由QH⊥HB得△HQB为直角三角形,从而可求H点的轨迹方程.
解答:
 解:(1)由题意知,双曲线4x2-
解:(1)由题意知,双曲线4x2- y2=1,∴c=1,
y2=1,∴c=1,∵椭圆的离心率为e=
 ,∴a=2,
,∴a=2,∴b2=a2-c2=3
∴椭圆方程为
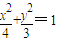 (3分)
(3分)(2)设M(x,y),P(4,z),则
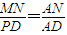 ,得
,得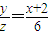 ,故
,故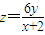 .
.设Q(x,0),由PQ⊥MB得:
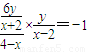 ,
,又M在椭圆上,故x2=4-
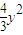 ,化简得
,化简得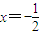 ,即Q(
,即Q(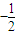 ,0)(8分)
,0)(8分)(3)点P在直线MB上射影即PQ与MB的交点H,由QH⊥HB得△HQB为直角三角形,
设E为QB中点,则|HE|=
 |QB|=
|QB|= ,E(
,E( ,0),
,0),因此H点的轨迹方程为
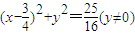 (13分)
(13分)点评:本题考查椭圆的标准方程,考查轨迹方程,解题的关键是确定椭圆中的几何量,利用垂直关系,建立等式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.