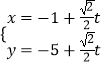题目内容
【题目】已知函数y=f(x)的定义域的R,当x<0时,f(x)>1,且对任意的实数x,y∈R,等式f(x)f(y)=f(x+y)成立,若数列{an}满足f(an+1)f( ![]() )=1(n∈N*),且a1=f(0),则下列结论成立的是( )
)=1(n∈N*),且a1=f(0),则下列结论成立的是( )
A.f(a2013)>f(a2016)
B.f(a2014)>f(a2017)
C.f(a2016)<f(a2015)
D.f(a2013)>f(a2015)
【答案】C
【解析】解:∵对任意的实数x,y∈R,f(x)f(y)=f(x+y)恒成立,
∴令x=﹣1,y=0,则f(﹣1)f(0)=f(﹣1),
∵当x<0时,f(x)>1,∴f(﹣1)≠0,则f(0)=1,
∵f(an+1)f( ![]() )=1=f(0),
)=1=f(0),
∴f(an+1+ ![]() )=f(0)=a1 , 则an+1+
)=f(0)=a1 , 则an+1+ ![]() =0,
=0,
即an+1=﹣ ![]() ,且a1=1,
,且a1=1,
当n=1时,a2=﹣ ![]() ;当n=2时,a3=﹣2;当n=3时,a4=1,
;当n=2时,a3=﹣2;当n=3时,a4=1,
∴数列{an}是以3为周期的周期数列,
∴a2013=a3=﹣2,a2014=a1=1,a2015=a2=﹣ ![]() ,
,
a2016=a3=﹣2,a2017=a1=1,
故选:C.

练习册系列答案
相关题目