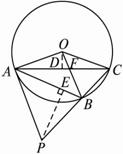
题目内容
如图(1)求证:BE·BF=BD·BC;
(2)试比较线段BD与AE的大小,并说明理由.
图
(1)证明:连结CF.
∵BC是直径,∴∠BFC=90°,
∵AD⊥BC,∴∠BDE=90°,∠B=∠B.
∴△BCF∽△BED.∴![]() .
.
∴BE·BF=BC·BD.
(2)解:AE>BD,证明如下:
连结AB、AC,则∠BAC=90°,
∵![]() =
=![]() ,∴∠ABF=∠ACB.
,∴∠ABF=∠ACB.
∵∠ACB+∠ABC=90°,∠BAD+∠ABD=90°,
∴∠ACB=∠BAD.∴∠ABF=∠BAD.
∴AE=BE.
在Rt△BDE中,BE>BD.∴AE>BD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
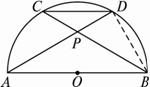
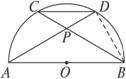
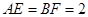 ,
,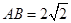 ,现将梯形沿CB、DA折起,使
,现将梯形沿CB、DA折起,使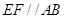 且
且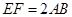 ,得一简单组合体
,得一简单组合体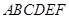 如图2示,已知
如图2示,已知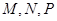 分别为
分别为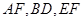 的中点.
的中点.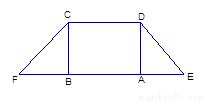
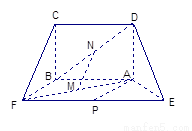
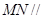 平面
平面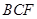 ;
;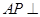
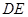 ;
; 多长时,平面
多长时,平面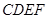 与平面
与平面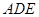 所成的锐二面角为
所成的锐二面角为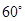 ?
?