题目内容
13.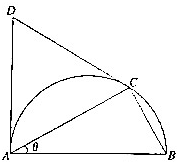 如图是一个半径为1的半圆,AB是直径,点C在圆弧上,且与A、B不重合,△ACD是等边三角形,设∠CAB=θ(0<θ<$\frac{π}{2}$),
如图是一个半径为1的半圆,AB是直径,点C在圆弧上,且与A、B不重合,△ACD是等边三角形,设∠CAB=θ(0<θ<$\frac{π}{2}$),(1)将三角形ABC的面积S1表示为θ的函数;
(2)将三角形ACD的面积S2表示为θ的函数;
(3)求四边形ABCD的面积S的最大值.
分析 (1)先由已知将AC,BC表示成θ的函数,求出△ABC的面积即可;
(2)由AC=2cosθ,即可求出等边三角形△ACD的面积;
(3)先求四边形ABCD的面积,根据数据函数的恒等变换,求S的最大值即可.
解答 解:(1)在△ABC中,AB是直径,
∴∠ACB=$\frac{π}{2}$;
∵∠CAB=θ(0<θ<$\frac{π}{2}$),
∴AC=AB•cos∠CAB=2cosθ,
BC=AB•sin∠CAB=2sinθ;
∴三角形ABC的面积S1=$\frac{1}{2}$AC•BC
=$\frac{1}{2}$×2cosθ×2sinθ
=2sinθcosθ
=sin2θ,
(2)等边三角形△ACD中,AC=2cosθ,
∴三角形ACD的面积S2=$\frac{1}{2}$×AC2•sin$\frac{π}{3}$=$\frac{1}{2}$×(2cosθ)2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$cos2θ
=$\frac{\sqrt{3}}{2}$cos2θ+$\frac{\sqrt{3}}{2}$;
(3)由(1),(2)可得四边形ABCD的面积为:S=S△ABC+S△ACD=sin2θ+$\frac{\sqrt{3}}{2}$cos2θ+$\frac{\sqrt{3}}{2}$;
∵S=sin2θ+$\frac{\sqrt{3}}{2}$cos2θ+$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{7}}{2}$sin(2θ+α)+$\frac{\sqrt{3}}{2}$,其中tanα=$\frac{\sqrt{3}}{2}$;
∴当2θ+α=$\frac{π}{2}$时,S取得最大值是$\frac{\sqrt{7}}{2}$+$\frac{\sqrt{3}}{2}$,此时θ=$\frac{π}{4}$-$\frac{1}{2}$arctan$\frac{\sqrt{3}}{2}$.
点评 本题考查了三角函数的恒等变换的应用问题,也考查了求三角形的面积的应用问题,是综合性题目.
