题目内容
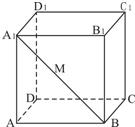
如图,正方体ABCD-A1B1C1D1的棱长为1,点M是对角线A1B上的动点,则AM+MD1的最小值为( )

A、
| ||||
B、2+
| ||||
C、
| ||||
| D、2 |
分析:欲求AM+MD1的最小值,先将展开平面ABA1和平面BCDD1A1放在同一个平面上,再利用两点之间线段最短,结合解三角形即可.
解答: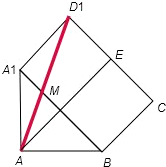 解:将平面ABA1和平面BCDD1A1放在同一个平面上,如图,
解:将平面ABA1和平面BCDD1A1放在同一个平面上,如图,
则AM+MD1的最小值即为线段AD1,
在直角三角形AED1 中,
AE=
+1,ED1=
,
∴AD1=
=
=
,
故选A.
 解:将平面ABA1和平面BCDD1A1放在同一个平面上,如图,
解:将平面ABA1和平面BCDD1A1放在同一个平面上,如图,则AM+MD1的最小值即为线段AD1,
在直角三角形AED1 中,
AE=
| ||
| 2 |
| ||
| 2 |
∴AD1=
| AE2+ED12 |
(
|
2+
|
故选A.
点评:本题主要考查了棱柱的结构特征、点、线、面间的距离计算,考查空间想象能力,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
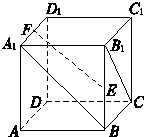 如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量
如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和A1D1的中点.证明:向量 如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.
如图,正方体ABCD-A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.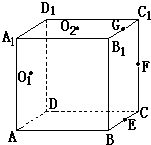 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,O1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点不在同一个平面上的是( )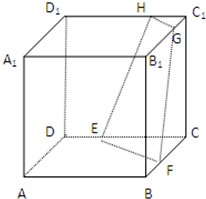 如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且
如图,正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱的三等分点,且