题目内容
3.设f(x)=ax2+bx+c(a>b>c),f(1)=0,g(x)=ax+b.(1)求证:-2<$\frac{c}{a}$<-$\frac{1}{2}$;
(2)设f(x)与g(x)交点A,B在x轴上投影为A1、B1,求|A1B1|的取值范围.
分析 (1)根据f(1)=0,得出a,b,c的关系,再由a>b>c进行证明;
(2)已知函数f(x)与g(x)的图象的两个交点A、B,由方程ax2+(b-a)x+c-b=0得出两根,根据韦达定理,进行求解.
解答 (1)证明:∵f(1)=0
∴a+b+c=0
∵a>b>c
∴a>0,c<0,a>-a-c>c,
∴-2<$\frac{c}{a}$<-$\frac{1}{2}$;
(2)解:由已知方程ax2+(b-a)x+c-b=0,两根为x1,x2,
x1+x2=$\frac{a-b}{a}$=2+$\frac{c}{a}$,x1x2=$\frac{c-b}{a}$=1+$\frac{2c}{a}$,
∴|x1-x2|=$\sqrt{(2+\frac{c}{a})^{2}-4(1+\frac{2c}{a})}$=$\sqrt{(\frac{c}{a}-2)^{2}-4}$
∵-2<$\frac{c}{a}$<-$\frac{1}{2}$,
∴|x1-x2|∈($\frac{3}{2}$,2$\sqrt{3}$).
点评 此题主要考查二次函数的图象及其性质的应用,第一问比较简单,第二问计算比较复杂,考查学生的计算能力,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知函数f(x)=$\frac{cx}{2x+3}$,x≠-$\frac{3}{2}$,且对于不等于-$\frac{3}{2}$的任何实数x,满足f[f(x)]=x,则实数c的值为( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
15.函数f(x)=(x-1)ex-x2的单调递减区间为( )
| A. | (-∞,-ln2)、(0,+∞) | B. | (0,ln2) | C. | (-∞,ln2) | D. | (-∞,0)、(ln2,+∞) |
12.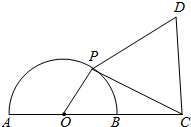 如图,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上一个动点,以DC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,则四边形OPDC面积的最大值为( )
如图,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上一个动点,以DC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,则四边形OPDC面积的最大值为( )
 如图,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上一个动点,以DC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,则四边形OPDC面积的最大值为( )
如图,已知半圆的直径AB=2,点C在AB的延长线上,BC=1,点P为半圆上一个动点,以DC为边作等边三角形PCD,且点D与圆心分别在PC的两侧,则四边形OPDC面积的最大值为( )| A. | 2 | B. | $\frac{5\sqrt{3}}{4}$-2 | C. | $\frac{5\sqrt{3}}{4}$ | D. | 2+$\frac{5\sqrt{3}}{4}$ |