题目内容
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且 .又以A、B为焦点的双曲线过C、D、E三点.若
.又以A、B为焦点的双曲线过C、D、E三点.若 ,则双曲线离心率e的取值范围为( )
,则双曲线离心率e的取值范围为( )
A.

B.

C.
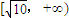
D.

【答案】分析:如图,在直角坐标系中,记双曲线的半焦距为c(c=2),h是梯形的高,用定比分点坐标公式可求得E点坐标x和y的表达式.设双曲线方程,将点C、E坐标和e分别代入双曲线方程联立后求得e和h的关系式,根据λ的范围求得e的范围.
解答: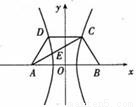 解:如图,以AB的垂直平分线为γ轴,直线AB为x轴,建立直角坐标系xOγ,则CD⊥γ轴.
解:如图,以AB的垂直平分线为γ轴,直线AB为x轴,建立直角坐标系xOγ,则CD⊥γ轴.
因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于γ轴对称,
设c为双曲线的半焦距(c=2),
依题意,记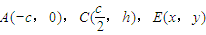 ,
,
h是梯形的高,
由定比分点坐标公式得 ,
,
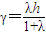 .
.
设双曲线的方程为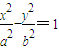 ,则离心率
,则离心率 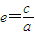 ,
,
由点C、E在双曲线上,将点C、E坐标和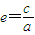 代入双曲线的方程,得
代入双曲线的方程,得 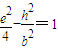 ,①
,①
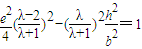 .②
.②
由①式得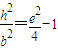 ,③
,③
将③式代入②式,整理得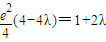 ,
,
故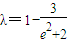
由题设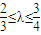 得,
得,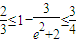 ,
,
解得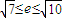 ,
,
所以,双曲线的离心率的取值范围为[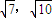 ].
].
故选A.
点评:本小题主要考查双曲线的简单性质、定比分点等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
解答:
 解:如图,以AB的垂直平分线为γ轴,直线AB为x轴,建立直角坐标系xOγ,则CD⊥γ轴.
解:如图,以AB的垂直平分线为γ轴,直线AB为x轴,建立直角坐标系xOγ,则CD⊥γ轴.因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于γ轴对称,
设c为双曲线的半焦距(c=2),
依题意,记
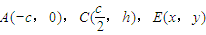 ,
,h是梯形的高,
由定比分点坐标公式得
 ,
,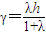 .
.设双曲线的方程为
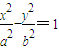 ,则离心率
,则离心率 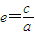 ,
,由点C、E在双曲线上,将点C、E坐标和
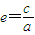 代入双曲线的方程,得
代入双曲线的方程,得 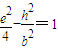 ,①
,①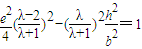 .②
.②由①式得
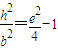 ,③
,③将③式代入②式,整理得
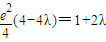 ,
,故
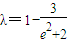
由题设
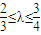 得,
得,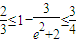 ,
,解得
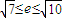 ,
,所以,双曲线的离心率的取值范围为[
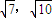 ].
].故选A.
点评:本小题主要考查双曲线的简单性质、定比分点等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
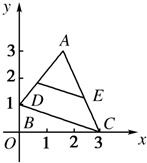 如图,已知A(2,3),B(0,1),C(3,0),点D,E分别在AB,AC上,DE∥BC,且DE平分△ABC的面积,求点D的坐标.
如图,已知A(2,3),B(0,1),C(3,0),点D,E分别在AB,AC上,DE∥BC,且DE平分△ABC的面积,求点D的坐标. 如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且 。又以A、B为焦点的双曲线过C、D、E三点。若
。又以A、B为焦点的双曲线过C、D、E三点。若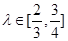 ,则双曲线离心率e的取值范围为( )
,则双曲线离心率e的取值范围为( )
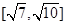 B.
B.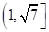 C.
C. D.
D.
 。又以A、B为焦点的双曲线过C、D、E三点。若
。又以A、B为焦点的双曲线过C、D、E三点。若 ,则双曲线离心率e的取值范围为( )
,则双曲线离心率e的取值范围为( )
 B.
B. C.
C. D.
D.