题目内容
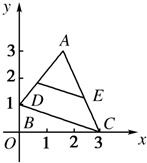如图，已知A（2，3），B（0，1），C（3，0），点D，E分别在AB，AC上，DE∥BC，且DE平分△ABC的面积，求点D的坐标．
分析：本题考查的知识点是线段的定比分点，要求点D坐标，关键是求得点D分
所成比λ的值，求λ值可由已知条件△ADE是△ABC面积一半入手，利用三角形面积比等于三角形相似比的平方关系求得λ，代入定比分点坐标公式，即可求出D点坐标．
| AB |
解答：解：∵DE∥BC，∴△ADE∽△ABC，
∴
=(
)2，
由已知，有(
)2=
，即
=
．
设点D分
所成的比为λ，利用分点定义，
得λ=
=
+1．
∴得点D的横、纵坐标为x=
=2-
，
y=
=3-
．
则点D坐标为（2-
，3-
）．
∴
| S△ADE |
| S△Abc |
| AD |
| AB |
由已知，有(
| AD |
| AB |
| 1 |
| 2 |
| AD |
| AB |
| 1 | ||
|
设点D分
| AB |
得λ=
| 1 | ||
|
| 2 |
∴得点D的横、纵坐标为x=
| 2 | ||
1+
|
| 2 |
y=
3+
| ||
1+
|
| 2 |
则点D坐标为（2-
| 2 |
| 2 |
点评：如果已知，有向线段A（x1，y1），B（x2，y2）．及点C分线段AB所成的比，求分点C的坐标，可将A，B两点的坐标代入定比分点坐标公式：坐标公式
进行求解．
|
练习册系列答案
相关题目
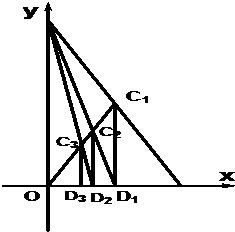如图，已知A（1，0），B（0，2），C1为AB的中点，O为坐标原点，过C1作C1D1⊥OA于D1点，连接BD1交OC1于C2点，过C2作C2D2⊥OA于D2点，连接BD2交OC1于C3点，过C3作C3D3⊥OA于D3点，如此继续，依次得到D1，D2，D3…Dn（n∈N*），记Dn的坐标为（an，0）．
如图，已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆（x-1）2+y2=1的交点，则|AB|•|CD|等于（ ）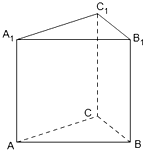
如图，已知A，B，C为不在同一直线上的三点，且AA1∥BB1∥CC1，AA1=BB1=CC1．