题目内容
.如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且 。又以A、B为焦点的双曲线过C、D、E三点。若
。又以A、B为焦点的双曲线过C、D、E三点。若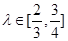 ,则双曲线离心率e的取值范围为( )
,则双曲线离心率e的取值范围为( )
A.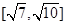 B.
B.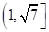 C.
C. D.
D.
A
解析考点:双曲线的简单性质.
分析:如图,在直角坐标系中,记双曲线的半焦距为c(c=2),h是梯形的高,用定比分点坐标公式可求得E点坐标x0和y0的表达式.设双曲线方程,将点C、E坐标和e分别代入双曲线方程联立后求得e和h的关系式,根据λ的范围求得e的范围.
解:如图,以AB的垂直平分线为γ轴,直线AB为x轴,建立直角坐标系xOγ,则CD⊥γ轴.
因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于γ轴对称,
设c为双曲线的半焦距(c=2),
依题意,记 A(-c,0),C( ,h),E(x0,y0),
,h),E(x0,y0),
h是梯形的高,
由定比分点坐标公式得 x0= =
= ,γ0=
,γ0= .
.
设双曲线的方程为  -
- =1,则离心率 e=
=1,则离心率 e= ,
,
由点C、E在双曲线上,将点C、E坐标和 e= 代入双曲线的方程,得
代入双曲线的方程,得  -
- =1,①
=1,① (
( )2-(
)2-( )2
)2 =1.②
=1.②
由①式得 =-1,③
=-1,③
将③式代入②式,整理得 (4-4λ)=1+2λ,
(4-4λ)=1+2λ,
故 λ=1-
由题设  ≤λ≤
≤λ≤ 得,
得, ≤1-
≤1- ≤
≤ ,
,
解得  ≤e≤
≤e≤ ,
,
所以,双曲线的离心率的取值范围为[ ,
, ].
].
故选A.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
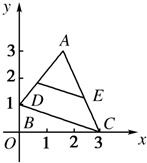 如图,已知A(2,3),B(0,1),C(3,0),点D,E分别在AB,AC上,DE∥BC,且DE平分△ABC的面积,求点D的坐标.
如图,已知A(2,3),B(0,1),C(3,0),点D,E分别在AB,AC上,DE∥BC,且DE平分△ABC的面积,求点D的坐标. 如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且 。又以A、B为焦点的双曲线过C、D、E三点。若
。又以A、B为焦点的双曲线过C、D、E三点。若 ,则双曲线离心率e的取值范围为( )
,则双曲线离心率e的取值范围为( )
 B.
B. C.
C. D.
D.
 .又以A、B为焦点的双曲线过C、D、E三点.若
.又以A、B为焦点的双曲线过C、D、E三点.若 ,则双曲线离心率e的取值范围为( )
,则双曲线离心率e的取值范围为( )