题目内容
(本题满分12分)已知向量 .
.
(1)当 时,求
时,求 的值;
的值;
(2)设函数 ,已知在△ABC中,内角A、B、C的对边分别为
,已知在△ABC中,内角A、B、C的对边分别为 ,若
,若 ,求
,求 (
( )的取值范围.
)的取值范围.
 .
.(1)当
 时,求
时,求 的值;
的值;(2)设函数
 ,已知在△ABC中,内角A、B、C的对边分别为
,已知在△ABC中,内角A、B、C的对边分别为 ,若
,若 ,求
,求 (
( )的取值范围.
)的取值范围.(1)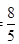 ;(2)
;(2)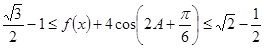 .
.
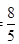 ;(2)
;(2)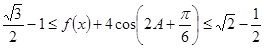 .
.本试题主要是考查了三角函数的化简以及关于解三角形的综合运用
第一问中,利用向量共线,然后得到三角函数关系式,从而得到角x的正切值。将所求的化简为关于正切值的函数表达式,得到。
第二问中,利用三角函数得到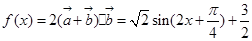
然后利用角的取值范围,结合三角函数的值域得到结论。
解:(1)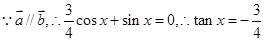 …………2分
…………2分
 …………6分
…………6分
(2)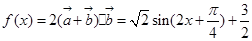
由正弦定理得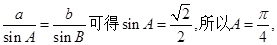 …………………9分
…………………9分

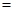
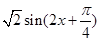
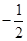 ,
,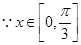
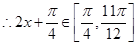 ,
,
所以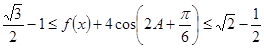 --------------------12分
--------------------12分
第一问中,利用向量共线,然后得到三角函数关系式,从而得到角x的正切值。将所求的化简为关于正切值的函数表达式,得到。
第二问中,利用三角函数得到
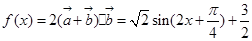
然后利用角的取值范围,结合三角函数的值域得到结论。
解:(1)
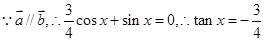 …………2分
…………2分 …………6分
…………6分(2)
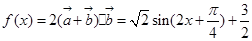
由正弦定理得
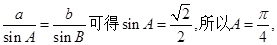 …………………9分
…………………9分
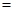
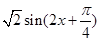
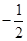 ,
,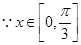
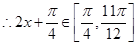 ,
, 所以
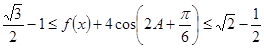 --------------------12分
--------------------12分
练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目

 的图象的一段,其解析式为 ;
的图象的一段,其解析式为 ;
 .
.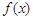 的最小正周期;
的最小正周期; ,求
,求 的值.
的值.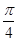 )的图像的一条对称轴是
)的图像的一条对称轴是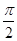

 ,将函数
,将函数 向左平移
向左平移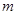 个单位
个单位 ,所得图象对应的函数为偶函数,则
,所得图象对应的函数为偶函数,则 ,
, ,则
,则 是( )
是( ) 的奇函数
的奇函数 的奇函数
的奇函数 ,
,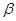 是第三象限的角,则
是第三象限的角,则 ________.
________.