题目内容
在平面直角坐标系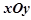 中,曲线
中,曲线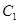 为
为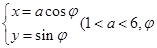 为参数)。在以
为参数)。在以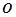 为原点,
为原点,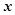 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线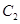 的极坐标方程为
的极坐标方程为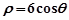 ,射线为
,射线为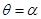 ,与
,与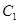 的交点为
的交点为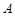 ,与
,与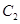 除极点外的一个交点为
除极点外的一个交点为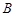 。当
。当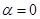 时,
时,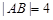 。
。
(1)求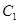 ,
,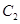 的直角坐标方程;
的直角坐标方程;
(2)设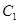 与
与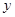 轴正半轴交点为
轴正半轴交点为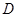 ,当
,当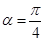 时,设直线
时,设直线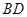 与曲线
与曲线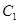 的另一个交点为
的另一个交点为 ,求
,求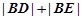 。
。
(1)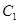 的直角坐标方程是
的直角坐标方程是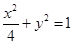 ,
,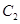 的直角坐标方程是
的直角坐标方程是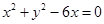 .(2)
.(2)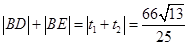
解析试题分析:(1)由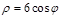 得
得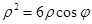 ,所以
,所以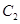 的直角坐标方程是
的直角坐标方程是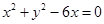 --2分
--2分
由已知得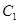 的直角坐标方程是
的直角坐标方程是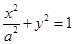 ,
,
当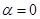 时射线与曲线
时射线与曲线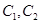 交点的直角坐标为
交点的直角坐标为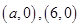 , 3分
, 3分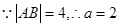
 的直角坐标方程是
的直角坐标方程是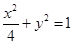 .① 5分
.① 5分
(2)联立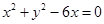 与
与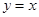 得
得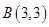 或
或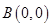 ,
,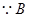 不是极点
不是极点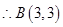 . 6分
. 6分
又可得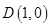 ,
, 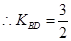
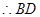 的参数方程为
的参数方程为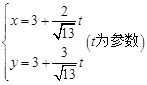 ② 8分
② 8分
将②带入①得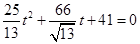 ,设
,设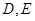 点的参数是
点的参数是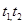 ,则
,则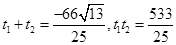
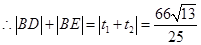 10分
10分
考点:本题考查了极坐标与直角坐标系的互化及参数的运用
点评:极坐标方面主要考查极坐标方程和直角坐标方程的互化、常见曲线的极坐标方程间的简单应用.在参数方程方面主要考查了参数方程所表示的曲线类型、参数法求最值的思想及平面几何中直线与圆等的位置关系问题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,以
,以 为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, 点的极坐标为
点的极坐标为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为
 为曲线
为曲线 中点
中点 到直线
到直线 (
( 为参数)距离的最小值.
为参数)距离的最小值. 的圆心
的圆心 ,半径
,半径
 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 两点,求弦长
两点,求弦长 的取值范围
的取值范围  的极坐标方程是
的极坐标方程是 ,直线的参数方程是
,直线的参数方程是 (为参数).
(为参数). 轴的交点是
轴的交点是 ,
, 是曲线
是曲线 的最大值.
的最大值. 经过点
经过点 ,圆心为直线
,圆心为直线 与极轴的交点,求圆
与极轴的交点,求圆 经过点
经过点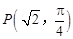 ,圆心为直线
,圆心为直线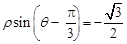 与极轴的交点,求圆
与极轴的交点,求圆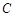 经过点
经过点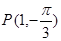 ,圆心为直线
,圆心为直线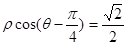 与极轴的交点,求圆
与极轴的交点,求圆 ,
, 、
、 分别是
分别是 两边上的动点。
两边上的动点。 ,
, 时,求
时,求 的长;
的长; 、
、 长度之和为定值4,求线段
长度之和为定值4,求线段