题目内容
(2012•河西区二模)已知椭圆
+
=1(a>b>0)的焦距为2
,离心率为
.
(Ⅰ)求椭圆方程;
(Ⅱ)设过椭圆顶点B(0,b),斜率为k的直线交椭圆于另一点D,交x轴于点E,且|BD|,|BE|,|DE|成等比数列,求k2的值.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 2 |
(Ⅰ)求椭圆方程;
(Ⅱ)设过椭圆顶点B(0,b),斜率为k的直线交椭圆于另一点D,交x轴于点E,且|BD|,|BE|,|DE|成等比数列,求k2的值.
分析:(Ⅰ)由已知2c=2
,
=
可求a,c结合b2=a2-c2=1即可求b,进而可求椭圆方程
(Ⅱ)由(Ⅰ)得过B点的直线为y=kx+1,联立直线y=kx+1与椭圆方程可求D的坐标,及k的取值范围,由|BD|,|BE|,|DE|成等比,可得|BE|2=|BD||DE|,即(1-yD)|yD|=1
,解方程可求
| 3 |
| c |
| a |
| ||
| 2 |
(Ⅱ)由(Ⅰ)得过B点的直线为y=kx+1,联立直线y=kx+1与椭圆方程可求D的坐标,及k的取值范围,由|BD|,|BE|,|DE|成等比,可得|BE|2=|BD||DE|,即(1-yD)|yD|=1
,解方程可求
解答: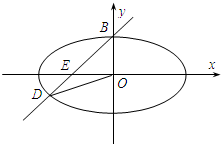 解:(Ⅰ)由已知2c=2
解:(Ⅰ)由已知2c=2
,
=
.…(2分)
解得a=2,c=
,…(4分)
所以b2=a2-c2=1,
椭圆的方程为
+y2=1.…(5分)
(Ⅱ)由(Ⅰ)得过B点的直线为y=kx+1,
由
得(4k2+1)x2+8kx=0,…(6分)
所以xD=-
,所以yD=
,…(8分)
依题意k≠0,k≠±
.
因为|BD|,|BE|,|DE|成等比数列,所以|BE|2=|BD||DE|,…(9分)
所以b2=(1-yD)|yD|,即(1-yD)|yD|=1,…(10分)
当yD>0时,yD2-yD+1=0,无解,…(11分)
当yD<0时,yD2-yD-1=0,解得yD=
,…(12分)
所以
=
,解得k2=
,
所以,当|BD|,|BE|,|DE|成等比数列时,k2=
.…(14分)
 解:(Ⅰ)由已知2c=2
解:(Ⅰ)由已知2c=2| 3 |
| c |
| a |
| ||
| 2 |
解得a=2,c=
| 3 |
所以b2=a2-c2=1,
椭圆的方程为
| x2 |
| 4 |
(Ⅱ)由(Ⅰ)得过B点的直线为y=kx+1,
由
|
所以xD=-
| 8k |
| 1+4k2 |
| 1-4k2 |
| 1+4k2 |
依题意k≠0,k≠±
| 1 |
| 2 |
因为|BD|,|BE|,|DE|成等比数列,所以|BE|2=|BD||DE|,…(9分)
所以b2=(1-yD)|yD|,即(1-yD)|yD|=1,…(10分)
当yD>0时,yD2-yD+1=0,无解,…(11分)
当yD<0时,yD2-yD-1=0,解得yD=
1-
| ||
| 2 |
所以
| 1-4k2 |
| 1+4k2 |
1-
| ||
| 2 |
2+
| ||
| 4 |
所以,当|BD|,|BE|,|DE|成等比数列时,k2=
2+
| ||
| 4 |
点评:本题主要考查了由椭圆的性质求解椭圆的方程,直线与椭圆的相交关系的应用,及等比数列的应用,属于综合性试题

练习册系列答案
相关题目
 (2012•河西区二模)阅读如图的程序框图,运行相应的程序,则输出的a的值为( )
(2012•河西区二模)阅读如图的程序框图,运行相应的程序,则输出的a的值为( )