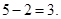题目内容
已知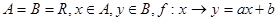 是从
是从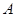 到
到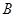 的映射,若1和8的原象分别是3和10,则5在
的映射,若1和8的原象分别是3和10,则5在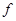 下的象是( )
下的象是( )
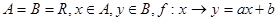 是从
是从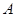 到
到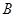 的映射,若1和8的原象分别是3和10,则5在
的映射,若1和8的原象分别是3和10,则5在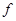 下的象是( )
下的象是( )| A.3 | B.4 | C.5 | D.6 |
A
试题分析:由题意可知
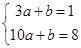 ,解得
,解得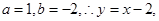 所以5在
所以5在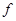 下的象是
下的象是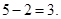
点评:准确理解映射的概念以及象与原象的概念是解决本小题的关键.

练习册系列答案
相关题目
题目内容
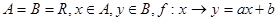 是从
是从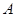 到
到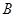 的映射,若1和8的原象分别是3和10,则5在
的映射,若1和8的原象分别是3和10,则5在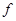 下的象是( )
下的象是( )| A.3 | B.4 | C.5 | D.6 |
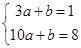 ,解得
,解得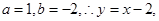 所以5在
所以5在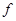 下的象是
下的象是