题目内容
3．在五边形ABCDE中，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AE}$=$\overrightarrow{b}$，$\overrightarrow{BC}$=$\overrightarrow{c}$，$\overrightarrow{ED}$=$\overrightarrow{d}$，用$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$、$\overrightarrow{d}$表示$\overrightarrow{CD}$．分析 运用向量加法的多边形法则，结合五边形ABCDE，即可得到所求．
解答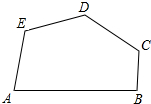 
解：由五边形ABCDE可得，$\overrightarrow{CD}$=$\overrightarrow{CB}$+$\overrightarrow{BA}$+$\overrightarrow{AE}$+$\overrightarrow{ED}$
=-$\overrightarrow{BC}$-$\overrightarrow{AB}$+$\overrightarrow{AE}$+$\overrightarrow{ED}$=-$\overrightarrow{c}$-$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{d}$．
即为$\overrightarrow{CD}$=-$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$+$\overrightarrow{d}$．
点评 本题考查向量加法的多边形法则，考查运算能力，属于基础题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
15．设f（x）=$\left\{\begin{array}{l}{\frac{|{x}^{2}-1|}{x-1}，x≠1}\\{2，x=1}\end{array}\right.$，则在点x=1处，函数f（x）（ ）
| A． | 不连续 | B． | 连续不可导 | ||
| C． | 可导且导数不连续 | D． | 可导且导数连续 |