题目内容
（本小题满分12分）在数列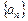
中，
，其中
．
(Ⅰ)求证：数列
为等差数列；
(Ⅱ)求证：
（Ⅰ）证明：
∴
数列为等差数列……………4分
（Ⅱ）因为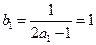
，所以
原不等式即为证明
，
即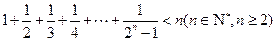
成立…………6分
用数学归纳法证明如下：
当
时，
成立,所以时，原不等式成立……………8分
假设当
时，
成立
当
时，
所以当时，不等式成立……………11分
所以对
，总有
成立……………12分
解析
练习册系列答案
相关题目
题目内容
（本小题满分12分）在数列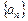中，，其中．
(Ⅰ)求证：数列为等差数列；
(Ⅱ)求证：
（Ⅰ）证明：
∴数列为等差数列……………4分
（Ⅱ）因为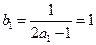，所以
原不等式即为证明，
即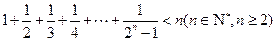成立…………6分
用数学归纳法证明如下：
当时，成立,所以时，原不等式成立……………8分
假设当时，成立
当时，
所以当时，不等式成立……………11分
所以对，总有成立……………12分
解析
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
