题目内容
以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线 的参数方程为
的参数方程为 (t为参数,0<a<
(t为参数,0<a< ),曲线C的极坐标方程为
),曲线C的极坐标方程为 .
.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A、B两点,当a变化时,求|AB|的最小值.
【答案】
(I) ;(II) 4.
;(II) 4.
【解析】
试题分析:(I)利用 ,易得曲线C的直角坐标方程
,易得曲线C的直角坐标方程 ;(II)直线过
;(II)直线过 点,根据直线的参数方程中
点,根据直线的参数方程中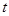 的几何意义,知道
的几何意义,知道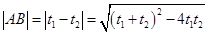 ,将直线的参数方程与抛物线方程联立,利用韦达定理转化为关于a的函数式,求最值即可.
,将直线的参数方程与抛物线方程联立,利用韦达定理转化为关于a的函数式,求最值即可.
试题解析:(I)由 ,得
,得 ,所以曲线C的直角坐标方程为
,所以曲线C的直角坐标方程为 ;
;
(II)将直线l的参数方程代入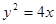 ,得
,得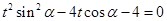 ,设
,设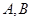 两点对应的参数分别为
两点对应的参数分别为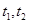 ,则
,则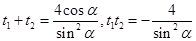 ,
,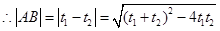

 ,当
,当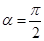 时,
时,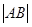 的最小值为
的最小值为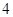 .
.
考点:1、极坐标方程与直角坐标方程的转化 2、直线的参数方程及应用 3、直线与圆锥曲线相交问题的综合应用 4、函数最值.

练习册系列答案
相关题目