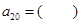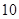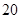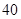题目内容
设递增等差数列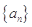 的前n项和为
的前n项和为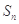 ,已知
,已知 ,
,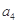 是
是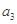 和
和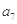 的等比中项.
的等比中项.
(l)求数列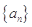 的通项公式;
的通项公式;
(2)求数列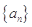 的前n项和
的前n项和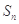 .
.
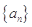 的前n项和为
的前n项和为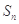 ,已知
,已知 ,
,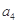 是
是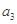 和
和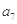 的等比中项.
的等比中项.(l)求数列
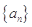 的通项公式;
的通项公式;(2)求数列
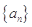 的前n项和
的前n项和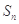 .
.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)先设出等差数列的首项和公差,然后根据等差数列的性质用首项和公差表示出
 ,
, 和
和 ,由已知条件“
,由已知条件“ 是
是 和
和 的等比中项”以及
的等比中项”以及 ,结合等比中项的性质列方程组
,结合等比中项的性质列方程组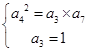 ,代入首项和公差,解方程组求解;(2)根据公式
,代入首项和公差,解方程组求解;(2)根据公式 ,将(1)中求得的首项和等差数列的通项公式代入此公式,化简求解.
,将(1)中求得的首项和等差数列的通项公式代入此公式,化简求解.试题解析:(1)在递增等差数列
 中,设公差为
中,设公差为 ,
,依题意可知
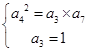 ,即
,即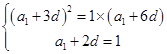 ,解得
,解得 , 6分
, 6分∴
 . 9分
. 9分(2)
 ,
, ∴所求为
 ,
, . 12分
. 12分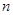 项和
项和
练习册系列答案
相关题目
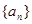 的前
的前 项和记为
项和记为 ,已知
,已知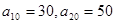 .
. ;
; ,求
,求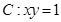 ,过
,过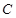 上一点
上一点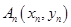 作一斜率为
作一斜率为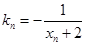 的直线交曲线
的直线交曲线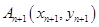 (
(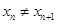 且
且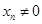 ,点列
,点列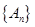 的横坐标构成数列
的横坐标构成数列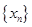 ,其中
,其中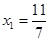 .
.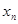 与
与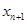 的关系式;
的关系式;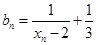 ,求证:数列
,求证:数列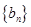 是等比数列;
是等比数列;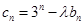 (
(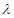 为非零整数,
为非零整数,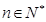 ),试确定
),试确定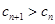 成立.
成立.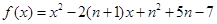 .
.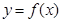 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列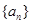 ,求证:
,求证: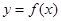 的图像的顶点到
的图像的顶点到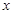 轴的距离构成数列
轴的距离构成数列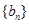 ,求
,求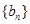 的前
的前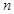 项和
项和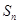 .
.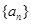 中,公差
中,公差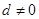 ,且
,且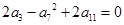 ,数列
,数列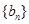 是等比数列,且
是等比数列,且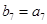 则
则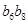 = .
= .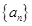 的递推公式
的递推公式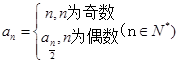 ,则
,则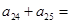 ;数列
;数列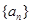 中,若
中,若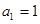 ,
,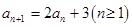 ,则该数列的通项
,则该数列的通项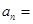 ________________.
________________.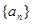 中,各项都是正数,且
中,各项都是正数,且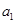 ,
,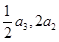 成等差数列,则
成等差数列,则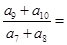 ( )
( )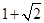
 为等差数列,
为等差数列,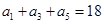 ,
,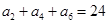 ,则
,则