题目内容
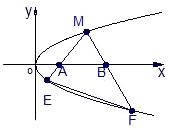 如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹方程.
分析:(1)可用待定系数法设出两直线的方程,用参数表示出两点E,F的坐标,用两点式求了过两点的直线的斜率,验证其是否与参数无关,若无关,则说明直线EF的斜率为定值.
(2)设出点M的坐标,如(1)用参数表示出点E,F的坐标,再由重心坐标与三角形的三个顶点的坐标之间的关系将其表示出来,消参数即可得重心的方程.
(2)设出点M的坐标,如(1)用参数表示出点E,F的坐标,再由重心坐标与三角形的三个顶点的坐标之间的关系将其表示出来,消参数即可得重心的方程.
解答:解:(1)设M(y02,y0),直线ME的斜率为k(k>0),则直线MF的斜率为-k
直线ME的方程为y-y0=k(x-y02),由
消去x得ky-y+y0(1-ky0)=0,解得yE=
,xE=
同理可得yF=
,xF=
∴kEF=
,将坐标代入得kEF=-
(定值)
所以直线EF的斜率为定值.
(2)当∠EMF=90°时,∠MAB=45°,所以k=1
∴直线ME的方程为:y-y0=x-y02,
由
得E((1-y0)2,1-y0)
同理可得F((1+y0)2,-(1+y0)),
设重心为G(x,y),则有
代入坐标得
消去参数y0得y2=
x-
(x>
)
直线ME的方程为y-y0=k(x-y02),由
|
消去x得ky-y+y0(1-ky0)=0,解得yE=
| 1-ky 0 |
| k |
| (1-ky 0) 2 |
| k 2 |
同理可得yF=
| 1+ky 0 |
| -k |
| (1+ky 0) 2 |
| k 2 |
∴kEF=
| y E-y F |
| X E-X F |
| 1 |
| 2y0 |
所以直线EF的斜率为定值.
(2)当∠EMF=90°时,∠MAB=45°,所以k=1
∴直线ME的方程为:y-y0=x-y02,
由
|
同理可得F((1+y0)2,-(1+y0)),
设重心为G(x,y),则有
|
代入坐标得
|
消去参数y0得y2=
| 1 |
| 9 |
| 2 |
| 27 |
| 2 |
| 3 |
点评:本题考点是直线与圆锥直线的位置关系,待定系数法表示方程,在本题验证直线过定点是先用参数表示出相关的直线方程解出两点的坐标再用斜率公式验证其是否为定值.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2
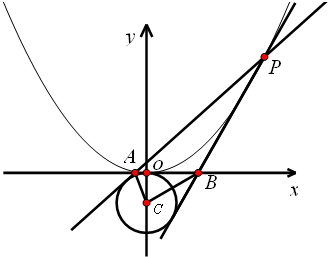
已知抛物线x2=2py(p>0).抛物线上的点M(m,1)到焦点的距离为2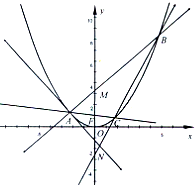 如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N. (2012•浙江模拟)已知抛物线x2=4y.
(2012•浙江模拟)已知抛物线x2=4y.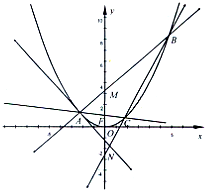 (2012•金华模拟)如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
(2012•金华模拟)如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.