题目内容
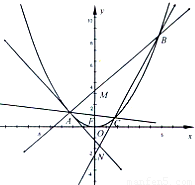
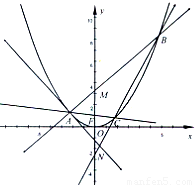
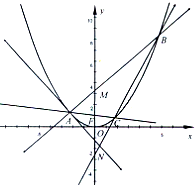 如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.(1)求证:|AF|=|MF|;
(2)求|MN|的最小值.
分析:(1)设A(x0,y0),B(x1,y1),C(x2,y2),求出直线l的斜率,可得AB的斜率,从而可得直线AB的方程,令x=0,确定M的坐标,从而可得|MF|=y0+1,由抛物线的定义可得|AF|=y0+1,则可得结论;
(2)先确定BC的斜率,进而可得BC的方程,进一步确定N的坐标,可得|MN|,利用基本不等式,可得|MN|的最小值.
(2)先确定BC的斜率,进而可得BC的方程,进一步确定N的坐标,可得|MN|,利用基本不等式,可得|MN|的最小值.
解答:(1)证明:设A(x0,y0),B(x1,y1),C(x2,y2),
∵x2=4y,∴y=
x2,∴y′=
x,∴直线l的斜率k1=
∵AB⊥l,∴kAB=-
,∴直线AB的方程为y-y0=-
(x-x0)
令x=0,则y=y0+2,∴M(0,y0+2)
∵F(0,1),∴|MF|=y0+1
由抛物线的定义可得|AF|=y0+1,
∴|AF|=|MF|;
(2)解:直线AB的方程代入抛物线方程,消去y可得
x2+
x-2-y0=0
∴x1+x0=-
,∴x1=-x0-
设直线AC:y=kx+1代入抛物线方程,消去y可得x2-4kx-4=0,∴x0x2=-4,∴x2=-
∴kBC=-
-
,∴直线BC的方程为y-y2=(-
-
)(x-x2)
令x=0得y=(-
-
)(-x2)+y2,代入x2=-
,y2=
,化简得y=-1-
∴N(0,-1-
),∴|MN|=y0+2+1+
=
+
3≥3+2
当且仅当x04=32时等号成立,
∴|MN|的最小值为3+2
.
∵x2=4y,∴y=
| 1 |
| 4 |
| 1 |
| 2 |
| x0 |
| 2 |
∵AB⊥l,∴kAB=-
| 2 |
| x0 |
| 2 |
| x0 |
令x=0,则y=y0+2,∴M(0,y0+2)
∵F(0,1),∴|MF|=y0+1
由抛物线的定义可得|AF|=y0+1,
∴|AF|=|MF|;
(2)解:直线AB的方程代入抛物线方程,消去y可得
| 1 |
| 4 |
| 2 |
| x0 |
∴x1+x0=-
| 8 |
| x0 |
| 8 |
| x0 |
设直线AC:y=kx+1代入抛物线方程,消去y可得x2-4kx-4=0,∴x0x2=-4,∴x2=-
| 4 |
| x0 |
∴kBC=-
| x0 |
| 4 |
| 3 |
| x0 |
| x0 |
| 4 |
| 3 |
| x0 |
令x=0得y=(-
| x0 |
| 4 |
| 3 |
| x0 |
| 4 |
| x0 |
| 4 | ||
|
| 8 | ||
|
∴N(0,-1-
| 8 | ||
|
| 8 | ||
|
| ||
| 4 |
| 8 | ||
|
| 2 |
∴|MN|的最小值为3+2
| 2 |
点评:本题考查抛物线的定义,考查直线方程的求解,考查直线与抛物线的位置关系,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
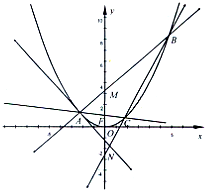 (2012•金华模拟)如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
(2012•金华模拟)如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.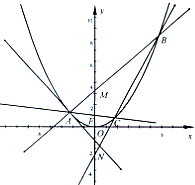 如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.
如图,A是抛物线x2=4y上异于原点的任意一点,F为抛物线的焦点,l为抛物线在A点处的切线,点B、C在抛物线上,AB⊥l且交y轴于M,点A、F、C三点共线,直线BC交y轴于N.