题目内容
已知抛物线x2=4y.(Ⅰ)过抛物线焦点F,作直线交抛物线于M,N两点,求|MN|最小值;
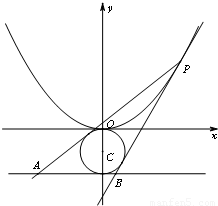
(Ⅱ)如图,P是抛物线上的动点,过P作圆C:x2+(y+1)2=1的切线交直线y=-2于A,B两点,当PB恰好切抛物线于点P时,求此时△PAB的面积.
【答案】分析:(Ⅰ)设PF的方程代入x2=4y,利用抛物线的定义,结合基本不等式,即可求得|MN|最小值;
(Ⅱ)求出抛物线在点P处切线方程,从而可求圆心C到该切线距离,由对称性,不妨设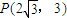 ,设切线方程,利用直线与圆相切,可得直线的斜率,进而可求|AB|,由此可求△PAB的面积.
,设切线方程,利用直线与圆相切,可得直线的斜率,进而可求|AB|,由此可求△PAB的面积.
解答:解:(Ⅰ)由题意F(0,1)
设M(x1,y1),N(x2,y2),PF的方程为y=kx+1代入x2=4y得x2-4kx-4=0
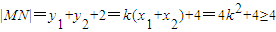
故当k=0时,|MN|min=4 …(5分)
(Ⅱ)设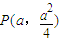 ,
, ,∴
,∴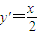
∴抛物线在点P处切线:
∴圆心C到该切线距离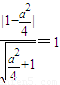 ,∴a2=12
,∴a2=12
由对称性,不妨设 …(9分)
…(9分)
显然过P作圆C的两条切线斜率都存在,设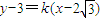 ,
,
∴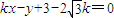
因为相切,所以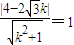
∴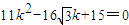
∴k=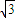 或
或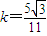
在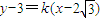 中,令y=-2,得x=
中,令y=-2,得x=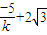 …(13分)
…(13分)
∴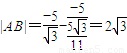
∴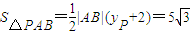 …(15分)
…(15分)
点评:本题考查抛物线中过焦点的弦长计算,考查抛物线的切线,正确运用抛物线的切线是关键.
(Ⅱ)求出抛物线在点P处切线方程,从而可求圆心C到该切线距离,由对称性,不妨设
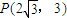 ,设切线方程,利用直线与圆相切,可得直线的斜率,进而可求|AB|,由此可求△PAB的面积.
,设切线方程,利用直线与圆相切,可得直线的斜率,进而可求|AB|,由此可求△PAB的面积.解答:解:(Ⅰ)由题意F(0,1)
设M(x1,y1),N(x2,y2),PF的方程为y=kx+1代入x2=4y得x2-4kx-4=0
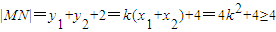
故当k=0时,|MN|min=4 …(5分)
(Ⅱ)设
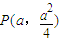 ,
, ,∴
,∴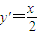
∴抛物线在点P处切线:

∴圆心C到该切线距离
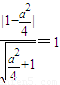 ,∴a2=12
,∴a2=12由对称性,不妨设
 …(9分)
…(9分)显然过P作圆C的两条切线斜率都存在,设
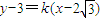 ,
,∴
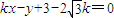
因为相切,所以
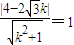
∴
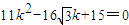
∴k=
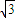 或
或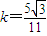
在
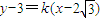 中,令y=-2,得x=
中,令y=-2,得x=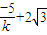 …(13分)
…(13分)∴
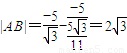
∴
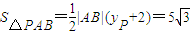 …(15分)
…(15分)点评:本题考查抛物线中过焦点的弦长计算,考查抛物线的切线,正确运用抛物线的切线是关键.

练习册系列答案
相关题目
 已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点.
已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点. (2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.
(2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F. (2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.
(2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.