题目内容
11.设集合A={x|$\frac{6}{x+1}$>1,x∈R},B={x|x2+mx+m2-7<0,x∈R,m∈R},C={y|y=$\frac{{x}^{2}}{{x}^{2}+1}$,x∈R}(Ⅰ)若集合A∩B=(-1,2),求m的值;
(Ⅱ)若C∪B=B,求m的取值范围.
分析 (Ⅰ)求出A中不等式的解集确定出A,根据B,以及A∩B=(-1,2),求出m的值即可;
(Ⅱ)根据B,C,以及C∪B=B,得到C为B的子集,列出关于m的不等式,求出不等式的解集即可确定出m的范围.
解答 解:(Ⅰ)由A中不等式变形得:$\frac{6}{x+1}$-1>0,即$\frac{x-5}{x+1}$<0,
解得:-1<x<5,即A=(-1,5),
∵B={x|x2+mx+m2-7<0,x∈R,m∈R},A∩B=(-1,2),
∴由题意知x=2是方程x2+mx+m2-7=0的根,得m=1或m=-3,
经检验m=-3不满足,m=1满足,
则m=1;
(Ⅱ)∵C={y|y=$\frac{{x}^{2}}{{x}^{2}+1}$,x∈R},
∴C=[0,1),
∵C⊆B,∴$\left\{\begin{array}{l}f(0)<0\\ f(1)≤0\end{array}\right.$,
解得:-$\sqrt{7}$<m≤2.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
2.等差数列{an}的前三项依次为a-1,a+1,2a+3,则此数列的第n项an=( )
| A. | 2n-5 | B. | 2n-3 | C. | 2n-1 | D. | 2n+1 |
16.函数f(x)=-x3-3x2-3x的单调减区间为( )
| A. | (0,+∞) | B. | (-∞,-1) | C. | (-∞,+∞) | D. | (-1,+∞) |
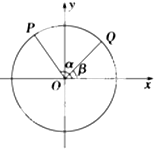 如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$
如图,以Ox为始边作角α与β(0<β<α<π),它们的终边分别与单位圆相交于P,Q两点,已知点P的坐标为$({-\frac{3}{5},\frac{4}{5}})$