题目内容
若函数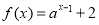 (其中
(其中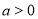 且
且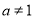 )的图像经过定点
)的图像经过定点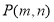 ,则
,则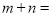 .
.
4
【解析】
试题分析:根据指数函数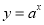 恒过定点
恒过定点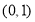 ,由
,由 ,令
,令 ,此时
,此时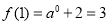 ,故函数
,故函数 的图像经过定点
的图像经过定点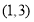 ,故
,故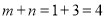 .
.
考点:指数函数性质的运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
若函数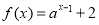 (其中
(其中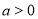 且
且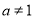 )的图像经过定点
)的图像经过定点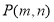 ,则
,则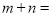 .
.
4
【解析】
试题分析:根据指数函数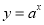 恒过定点
恒过定点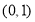 ,由
,由 ,令
,令 ,此时
,此时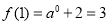 ,故函数
,故函数 的图像经过定点
的图像经过定点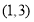 ,故
,故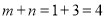 .
.
考点:指数函数性质的运用.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案