题目内容
已知函数f(x)=x3+2bx2+cx-2的图象在与x轴交点处的切线方程是y=5x-10.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+mx,若g(x)的极值存在,求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值.
【答案】
解:(1)由已知,得切点为(2,0),故有f(2)=0,
即4b+c+3=0,①
f′(x)=3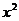 +4
+4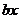 +c,由已知,得f′(2)=12+8b+c=5.即8b+c+7=0.②
+c,由已知,得f′(2)=12+8b+c=5.即8b+c+7=0.②
联立①、②,解得b=-1,c=1,
于是函数解析式为f(x)=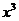 -2
-2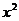 +x-2.
+x-2.
(2)g(x)=f(x)+mx=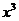 -2
-2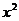 +x-2+mx,g′(x)=3
+x-2+mx,g′(x)=3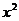 -4x+1+,令g′(x)=0.
-4x+1+,令g′(x)=0.
当函数有极值时,Δ≥0,方程3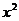 -4x+1+=0有实根,
-4x+1+=0有实根,
由Δ=4(1-m)≥0,得m≤1.
①当m=1时,g′(x)=0有实根x=,在x=左右两侧均有g′(x)>0,故函数g(x)无极值.
②当m<1时,g′(x)=0有两个实根,
 =(2-),
=(2-),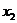 =(2+),
=(2+),
当x变化时,g′(x)、g(x)的变化情况如下表:
|
x |
(-∞, |
|
( |
|
( |
|
g′(x) |
+ |
0 |
- |
0 |
+ |
|
g(x) |
? |
极大值 |
? |
极小值 |
? |
故在m∈(-∞,1)时,函数g(x)有极值:
当x=(2-)时,g(x)有极大值;
当x=(2+)时,g(x)有极小值.

练习册系列答案
相关题目
 g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围. x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0. ax2+3x.
ax2+3x.