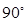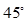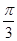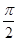题目内容
如图所示,在正三棱柱ABC-A1B1C1中,AB=1.若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( ).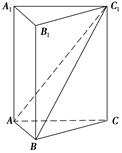
A. | B.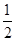 | C.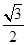 | D.1 |
A
解析

练习册系列答案
相关题目
设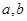 是两条不同的直线,
是两条不同的直线,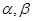 是两个不同的平面,则能得出
是两个不同的平面,则能得出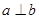 的是( )
的是( )
A.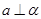 , , , ,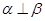 | B.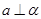 , ,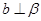 , , |
C. , ,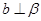 , , | D. , , , ,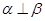 |
设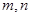 是两条不同的直线,
是两条不同的直线,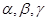 是三个不同的平面,下列四个命题中假命题的是( )
是三个不同的平面,下列四个命题中假命题的是( )
A.若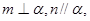 则 则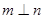 | B.若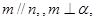 则 则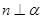 |
C.若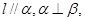 则 则 | D.若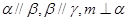 ,则 ,则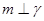 |
如图,正方体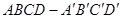 中,
中,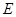 是棱
是棱 的中点,
的中点,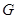 是棱
是棱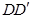 的中点,则异面直线
的中点,则异面直线 与
与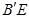 所成的角为
所成的角为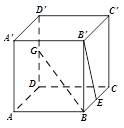
A.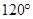 | B.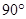 |
C.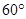 | D.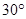 |
设α,β是两个不同的平面,l是一条直线,以下命题正确的是( )
| A.若l⊥α,α⊥β,则l?β | B.若l∥α,α∥β,则l?β |
| C.若l⊥α,α∥β,则l⊥β | D.若l∥α,α⊥β,则l⊥β |
如图所示,在四边形A-BCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥ABCD,则在三棱锥ABCD中,下列命题正确的是( ).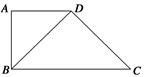
| A.平面ABD⊥平面ABC |
| B.平面ADC⊥平面BDC |
| C.平面ABC⊥平面BDC |
| D.平面ADC⊥平面ABC |
下列命题中错误的是 ( ).
| A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β |
| B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
| C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ |
| D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β |