题目内容
数列{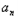 }中,a1=8,a4=2,且满足
}中,a1=8,a4=2,且满足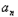 +2﹣2
+2﹣2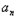 +1+
+1+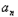 =0,n∈N.
=0,n∈N.
(1)求数列{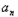 }的通项;
}的通项;
(2)设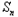 =|a1|+|a2|+…+|
=|a1|+|a2|+…+|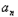 |,求
|,求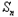 .
.
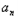 }中,a1=8,a4=2,且满足
}中,a1=8,a4=2,且满足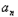 +2﹣2
+2﹣2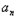 +1+
+1+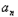 =0,n∈N.
=0,n∈N.(1)求数列{
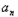 }的通项;
}的通项;(2)设
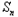 =|a1|+|a2|+…+|
=|a1|+|a2|+…+|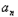 |,求
|,求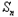 .
.解:(1)由题意,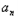 +2﹣
+2﹣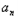 +1=
+1=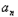 +1﹣
+1﹣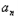 ,
,
∴数列{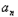 }是以8为首项,﹣2为公差的等差数列
}是以8为首项,﹣2为公差的等差数列
∴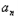 =10﹣2n,n∈N
=10﹣2n,n∈N
(2)∵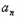 =10﹣2n,
=10﹣2n,
令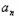 =0,得n=5.
=0,得n=5.
当n>5时, <0;
<0;
当n=5时,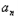 =0;
=0;
当n<5时, >0.
>0.
∴当n>5时,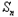 =|a1|+|a2|+…+|
=|a1|+|a2|+…+| |=a1+a2+…+a5﹣(a6+a7+…+
|=a1+a2+…+a5﹣(a6+a7+…+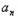 )
)
=T5﹣(Tn﹣T5)=2T5﹣Tn,Tn=a1+a2+…+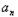 .
.
当n≤5时, =|a1|+|a2|+…+|
=|a1|+|a2|+…+| |=a1+a2+…+
|=a1+a2+…+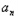 =Tn.
=Tn.
∴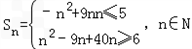
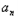 +2﹣
+2﹣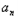 +1=
+1=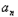 +1﹣
+1﹣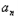 ,
,∴数列{
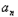 }是以8为首项,﹣2为公差的等差数列
}是以8为首项,﹣2为公差的等差数列∴
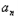 =10﹣2n,n∈N
=10﹣2n,n∈N(2)∵
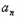 =10﹣2n,
=10﹣2n,令
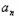 =0,得n=5.
=0,得n=5.当n>5时,
 <0;
<0;当n=5时,
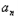 =0;
=0;当n<5时,
 >0.
>0.∴当n>5时,
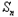 =|a1|+|a2|+…+|
=|a1|+|a2|+…+| |=a1+a2+…+a5﹣(a6+a7+…+
|=a1+a2+…+a5﹣(a6+a7+…+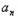 )
)=T5﹣(Tn﹣T5)=2T5﹣Tn,Tn=a1+a2+…+
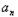 .
.当n≤5时,
 =|a1|+|a2|+…+|
=|a1|+|a2|+…+| |=a1+a2+…+
|=a1+a2+…+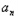 =Tn.
=Tn.∴

练习册系列答案
相关题目