题目内容
如图,设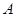 是棱长为
是棱长为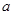 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有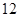 个顶点;②有
个顶点;②有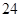 条棱;③有
条棱;③有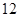 个面;④表面积为
个面;④表面积为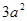 ;⑤体积为
;⑤体积为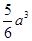 .其中正确的结论是____________.(要求填上所有正确结论的序号)
.其中正确的结论是____________.(要求填上所有正确结论的序号)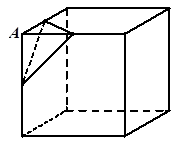
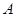 是棱长为
是棱长为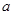 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有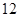 个顶点;②有
个顶点;②有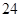 条棱;③有
条棱;③有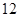 个面;④表面积为
个面;④表面积为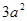 ;⑤体积为
;⑤体积为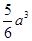 .其中正确的结论是____________.(要求填上所有正确结论的序号)
.其中正确的结论是____________.(要求填上所有正确结论的序号)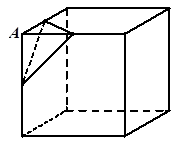
①②⑤
解:如图,
原来的六个面还在只不过是变成了一个小正方形,再添了八个顶点各对应的一个三角形的面,所以总计6+8=14个面,故③错;
每个正方形4条边,每个三角形3条边,4×6+3×8=48,考虑到每条边对应两个面,所以实际只有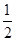 ×48=24条棱.②正确;
×48=24条棱.②正确;
所有的顶点都出现在原来正方体的棱的中点位置,
原来的棱的数目是12,所以现在的顶点的数目是12.
或者从图片上可以看出每个顶点对应4条棱,每条棱很明显对应两个顶点,所以顶点数是棱数的一半即12个.①正确;
三角形和四边形的边长都是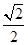 a,所以正方形总面积为6×
a,所以正方形总面积为6×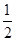 ×a2=3a2,三角形总面积为8×
×a2=3a2,三角形总面积为8×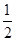 ×
×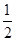 a2sin60°=
a2sin60°= a2,表面积(3+
a2,表面积(3+ )a2,故④错;
)a2,故④错;
体积为原正方形体积减去8个三棱锥体积,每个三棱锥体积为8× (
( )3=
)3= a2,剩余总体积为a3-
a2,剩余总体积为a3- a3=
a3=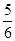 a3⑤正确.
a3⑤正确.
故答案为:①②⑤.
原来的六个面还在只不过是变成了一个小正方形,再添了八个顶点各对应的一个三角形的面,所以总计6+8=14个面,故③错;
每个正方形4条边,每个三角形3条边,4×6+3×8=48,考虑到每条边对应两个面,所以实际只有
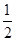 ×48=24条棱.②正确;
×48=24条棱.②正确;所有的顶点都出现在原来正方体的棱的中点位置,
原来的棱的数目是12,所以现在的顶点的数目是12.
或者从图片上可以看出每个顶点对应4条棱,每条棱很明显对应两个顶点,所以顶点数是棱数的一半即12个.①正确;
三角形和四边形的边长都是
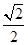 a,所以正方形总面积为6×
a,所以正方形总面积为6×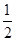 ×a2=3a2,三角形总面积为8×
×a2=3a2,三角形总面积为8×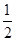 ×
×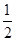 a2sin60°=
a2sin60°= a2,表面积(3+
a2,表面积(3+ )a2,故④错;
)a2,故④错;体积为原正方形体积减去8个三棱锥体积,每个三棱锥体积为8×
 (
( )3=
)3= a2,剩余总体积为a3-
a2,剩余总体积为a3- a3=
a3=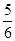 a3⑤正确.
a3⑤正确.故答案为:①②⑤.

练习册系列答案
相关题目
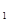 B
B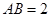 ,
,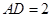 ,
,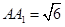 ,则点
,则点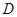 到平面
到平面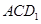 的距离是( )
的距离是( ) 

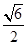


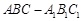 中,侧面
中,侧面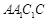
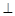 底面
底面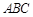 ,
,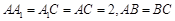 ,且
,且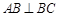 ,O为
,O为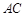 中点.
中点.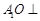 平面
平面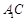 与平面
与平面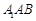 所成角的正弦值
所成角的正弦值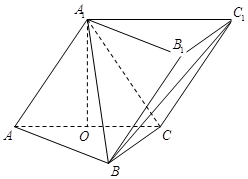








 +
+