题目内容
下列命题中,真命题的个数为( )
(1)在△ABC中,若A>B,则sinA>sinB;
(2)已知
=(3,4),
=(-2,-1),则
在
上的投影为-2;
(3)已知p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧¬q”为假命题;
(4)已知函数f(x)=sin(ωx+
)-2(ω>0)的导函数的最大值为3,则函数f(x)的图象关于x=
对称.
(1)在△ABC中,若A>B,则sinA>sinB;
(2)已知
| AB |
| CD |
| AB |
| CD |
(3)已知p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧¬q”为假命题;
(4)已知函数f(x)=sin(ωx+
| π |
| 6 |
| π |
| 3 |
分析:对于(1)利用分类讨论,利用诱导公式确定A>B,则sinA>sinB的正确性.
对于(2)先求得向量的坐标,再求得其数量积和模,然后用投影公式求解.判断即可.
对于(3)分别判断两个命题的正误即可.
对于(4)求出ω,通过条件求解结果,判断正误即可.
对于(2)先求得向量的坐标,再求得其数量积和模,然后用投影公式求解.判断即可.
对于(3)分别判断两个命题的正误即可.
对于(4)求出ω,通过条件求解结果,判断正误即可.
解答:解:(1)在△ABC中,若A>B,则sinA>sinB;此是一个真命题,
若A>B,当A不超过90°时,显然可得出sinA>sinB,
当A是钝角时,由于
>π-A>B,可得sin(π-A)=sinA>sinB,即 A>B⇒sinA>sinB.正确.
(2)已知
=(3,4),
=(-2,-1),|
|=5,|
|=
,
cosα=
=-
≠2,则
在
上的投影为-2,不正确.
(3)p:?x∈R,cosx=1,正确;q:?x∈R,x2-x+1>0,正确,所以¬q不正确,则“p∧¬q”为假命题,正确.
(4)函数f(x)=sin(ωx+
)-2(ω>0)的导函数的最大值为3,所以ω=3,当x=
时,函数值为-
,不是最值,所以函数f(x)的图象关于x=
对称,显然不正确.
故选B.
若A>B,当A不超过90°时,显然可得出sinA>sinB,
当A是钝角时,由于
| π |
| 2 |
(2)已知
| AB |
| CD |
| AB |
| CD |
| 5 |
| AB |
| ||||
|
|
| 10 | ||
|
| AB |
| CD |
(3)p:?x∈R,cosx=1,正确;q:?x∈R,x2-x+1>0,正确,所以¬q不正确,则“p∧¬q”为假命题,正确.
(4)函数f(x)=sin(ωx+
| π |
| 6 |
| π |
| 3 |
| 5 |
| 2 |
| π |
| 3 |
故选B.
点评:本题考查命题的正误,向量的数量积的应用,三角函数的对称轴的应用,考查基本知识的灵活运用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
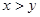 ,则
,则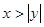 ”的逆命题
”的逆命题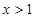 ,则
,则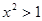 ”的否命题
”的否命题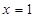 ,则
,则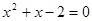 ”的否命题
”的否命题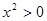 ,则
,则