题目内容
5.在抛物线y2=2x中,焦点到准线的距离为a,若实数x,y满足$\left\{\begin{array}{l}{x-y+1≥o}\\{x+y≥0}\\{x≤a}\end{array}\right.$,则z=x+2y的最小值是( )| A. | -1 | B. | $\frac{1}{2}$ | C. | 5 | D. | 1 |
分析 在抛物线y2=2x中,焦点到准线的距离a=p=1,已知实数x,y满足$\left\{\begin{array}{l}{x-y+1≥o}\\{x+y≥0}\\{x≤a}\end{array}\right.$,即$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤1}\end{array}\right.$.画出图象及其目标函数,即可得出.
解答 解:在抛物线y2=2x中,焦点到准线的距离a=p=1,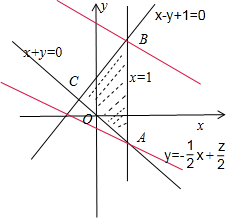
∵实数x,y满足$\left\{\begin{array}{l}{x-y+1≥o}\\{x+y≥0}\\{x≤a}\end{array}\right.$,即$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤1}\end{array}\right.$.
画出图象:
联立$\left\{\begin{array}{l}{x=1}\\{x+y=0}\end{array}\right.$,解得A(1,-1).
由z=x+2y变为y=-$\frac{1}{2}$x+$\frac{z}{2}$,画出目标函数.
可知:当目标函数经过点A(1,-1)时,z取得最小值-1.
故选:A.
点评 本题考查了抛物线的标准方程及其性质、线性规划的有关知识,考查了数形结合的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.直线y=kx+2与抛物线y2=8x只有一个公共点,则k的值为( )
| A. | 1 | B. | 0 | C. | 1或0 | D. | 1或3 |
10.已知点A(-1,0)以及抛物线y2=4x的焦点F,若P是抛物线上的动点,则$\frac{|PF|}{|PA|}$的取值范围是( )
| A. | [0,$\frac{\sqrt{2}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1] | C. | ($\frac{\sqrt{2}}{2}$,1] | D. | ($\frac{\sqrt{2}}{2}$,1) |
 已知抛物线C:x2=4y和直线l:y=-2,直线l与y轴的交点为D,过点Q(0,2)的直线交抛物线C于A,B两点,与直线l交于点P.
已知抛物线C:x2=4y和直线l:y=-2,直线l与y轴的交点为D,过点Q(0,2)的直线交抛物线C于A,B两点,与直线l交于点P. 如图,过抛物线C:y2=2px(p>0)焦点F的直线与C交于 M,N两点,直线x=4交抛物线C于 A,B两点,点 M,N在直线x=4的同侧.已知|AF|=5,四边形AMNB的面积为$\frac{133}{8}$.
如图,过抛物线C:y2=2px(p>0)焦点F的直线与C交于 M,N两点,直线x=4交抛物线C于 A,B两点,点 M,N在直线x=4的同侧.已知|AF|=5,四边形AMNB的面积为$\frac{133}{8}$. 端午节即将到来,为了做好端午节商场促销活动,某商场打算将进行促销活动的礼品盒重新设计.方案如下:将一块边长为10的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′再将剩下的阴影部分折成一个四棱锥形状的包装盒S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示).
端午节即将到来,为了做好端午节商场促销活动,某商场打算将进行促销活动的礼品盒重新设计.方案如下:将一块边长为10的正方形纸片ABCD剪去四个全等的等腰三角形△SEE′,△SFF′,△SGG′,△SHH′再将剩下的阴影部分折成一个四棱锥形状的包装盒S-EFGH,其中A,B,C,D重合于点O,E与E′重合,F与F′重合,G与G′重合,H与H′重合(如图所示).