题目内容
9.已知直线l:x+my+4=0,若曲线x2+y2+2x-6y+1=0上存在两点P、Q关于直线l对称,则m的值为-1.分析 曲线x2+y2+2x-6y+1=0上有两点P、Q,满足关于直线x+my+4=0对称,说明曲线是圆,直线过圆心,易求m的值
解答 解:曲线方程为(x+1)2+(y-3)2=9表示圆心为(-1,3),半径为3的圆.
∵点P、Q在圆上且关于直线x+my+4=0对称,
∴圆心(-1,3)在直线上.代入得m=-1.
故答案为:-1.
点评 本题考查直线与圆的方程的应用,圆的一般式方程,考查函数与方程的思想,是中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
14.在等差数列{an}中,若3(a4+a6)+2(a7+a9+a11)=24,则此数列的前13项之和为( )
| A. | 13 | B. | 26 | C. | 52 | D. | 156 |
1. 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
(Ⅰ)完成频率分布表,并画出频率分布直方图;
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
 在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.
在生产过程中,测得100件纤维产品的纤度(表示纤维粗细的一种量),将数据分组如表.| 分组 | 频数 | 频率 |
| [1.30,1.34) | 4 | |
| [1.34,1.38) | 25 | |
| [1.38,1.42) | 30 | |
| [1.42,1.46) | 29 | |
| [1.46,1.50) | 10 | |
| [1.50,1.54) | 2 | |
| 合计 | 100 |
(Ⅱ)从纤度最小、最大的6件产品中任取2件,设取出的纤度在[1.30,1.34)内的产品有ξ件,求ξ的分布列和期望.
18.已知全集U={x||x|≤2},A={x|x2+x-2≤0},则∁UA=( )
| A. | {x|1≤x≤2} | B. | {x|1<x≤2} | C. | {x|-1≤x≤2} | D. | {x|-1<x≤2} |
18.函数y=$\sqrt{{x}^{2}-4x+13}$-$\sqrt{{x}^{2}+1}$的最大值是( )
| A. | 2$\sqrt{2}$ | B. | 10 | C. | $\sqrt{10}$ | D. | 0 |
 中,
中,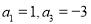 ,则
,则 ____________.
____________.