题目内容
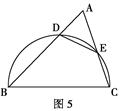
有一张矩形纸片ABCD,其中AD=8cm,上面有一个以AD为直径的半圆,正好与对边BC相切.如图(甲).将它沿DE折叠,使A点落在BC上,如图(乙),这时,半圆还露在外面的部分(阴影部分)的面积是【 】
A.(π- )cm2 )cm2 | B.(  π- π- ) ) |
C.( π+ π+ ) ) | D.( π+ π+ ) ) |
B
解析试题分析:
由图可得,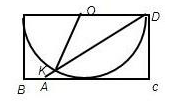
∠DAC=30°,∠KOD=120°,可得S阴影=S扇形-S△OKD,过O作OM⊥DK,因为OK=2,OM=1,DK="2MK=2" ,求得S扇形,S△OKD即可得到为(  π-
π- )
) ,故选B.
,故选B.
考点:扇形面积和三角形面积
点评:利用已知图形的折叠来分析阴影部分的面积与杀那个行和

练习册系列答案
相关题目
如图,在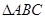 和
和 中,
中, ,若
,若 与
与 的周长之差为
的周长之差为 ,则
,则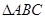 的周长为( )
的周长为( )
A. 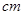 | B.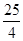 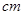 | C.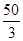  | D.25 |
已知四棱锥底面四边形中顺次三个内角的大小之比为 ,此棱锥的侧棱与底面所成的角相等,则底面四边形的最小角是( ).
,此棱锥的侧棱与底面所成的角相等,则底面四边形的最小角是( ).
A. | B. | C. | D.无法确定的 |
如图, 的外接圆的圆心为
的外接圆的圆心为 ,
, , 则
, 则 等于( )
等于( )
A. | B. | C.2 | D.3 |
如图所示,PC与圆O相切于点C,直线PO交圆O于A,B两点,弦CD垂直AB于E,则下面结论中,错误的结论是( )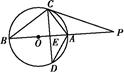
| A.△BEC∽△DEA |
| B.∠ACE=∠ACP |
| C.DE2=OE·EP |
| D.PC2=PA·AB |
已知圆的半径为6.5 cm,圆心到直线l的距离为4.5 cm,那么这条直线和这个圆的公共点的个数是
| A.0 | B.1 | C.2 | D.不能确定 |
若 =
= ,则下列各式一定成立的是
,则下列各式一定成立的是
A.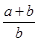 = =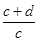 | B.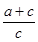 = = |
C. = = | D.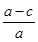 = = |
 是圆
是圆 的切线,切点为
的切线,切点为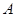 ,
, 交圆
交圆 、
、 两点,且
两点,且 ,
, ,则
,则 的长为 .
的长为 .