题目内容
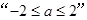 是“实系数一元二次方程
是“实系数一元二次方程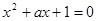 有虚根”的( )
有虚根”的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:因为实系数一元二次方程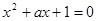 有虚跟,
有虚跟,
所以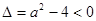 ,解得
,解得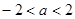 ,所以
,所以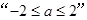 是“
是“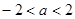 ”的必要不充分条件.故选A.
”的必要不充分条件.故选A.
考点:必要条件 充分条件 充要条件的判断
点评:本题考查必要条件 充分条件和充要条件的应用,解题时应严格按定义来判断,认真审题,仔细解答.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
设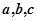 分别
分别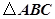 是的三个内角
是的三个内角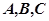 所对的边,若
所对的边,若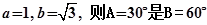 的( )
的( )
| A.充分不必要条件; | B.必要不充分条件; |
| C.充要条件; | D.既不充分也不必要条件; |
下列命题中错误的是
A.命题“若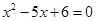 ,则 ,则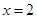 ”的逆否命题是“若 ”的逆否命题是“若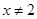 ,则 ,则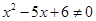 ” ” |
B.对命题 : : ,使得 ,使得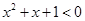 ,则 ,则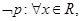 则 则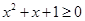 |
C.已知命题p和q,若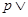 q为假命题,则命题p与q中必一真一假 q为假命题,则命题p与q中必一真一假 |
D.若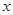 、 、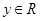 ,则“ ,则“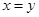 ”是“ ”是“ ”成立的充要条件 ”成立的充要条件 |
“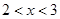 ”是“
”是“ ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列命题正确的是 ( )
| A.很小的实数可以构成集合。 |
B.集合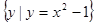 与集合 与集合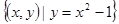 是同一个集合。 是同一个集合。 |
C.自然数集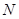 中最小的数是 中最小的数是 。 。 |
| D.空集是任何集合的子集。 |
已知命题“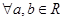 ,如果
,如果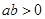 ,则
,则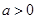 ”,则它的否命题是
”,则它的否命题是
A.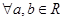 ,如果 ,如果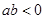 ,则 ,则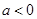 |
B.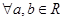 ,如果 ,如果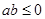 ,则 ,则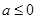 |
C.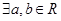 ,如果 ,如果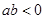 ,则 ,则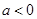 |
D.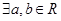 ,如果 ,如果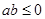 ,则 ,则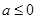 |
原命题:“设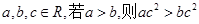 ”以及它的逆命题、否命题、逆否命题中,真命题共有( )个.
”以及它的逆命题、否命题、逆否命题中,真命题共有( )个.
| A.0 | B.1 | C.2 | D.4 |
若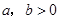 ,则
,则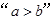 是“
是“ ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分且必要条件 | D.既非充分也非必要条件 |
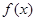 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,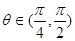 ,则
,则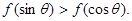
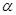 、
、