题目内容
1.若函数f(x)满足f(xy)=f(x)+f(y),且f(2)=m,f(3)=n,则f(36)=( )| A. | 6mn | B. | m3+n2 | C. | 2m+2n | D. | 3m+2n |
分析 利用赋值法f(36)=2f(6)=2[f(2)+f(3)],把已知代入即可求解.
解答 解:∵f(xy)=f(x)+f(y),f(2)=m,f(3)=n,
∴f(36)=2f(6)=2[f(2)+f(3)]=2(m+n)
故选:C.
点评 本题主要考查了抽象函数中利用赋值求解函数值,属于基础试题

练习册系列答案
相关题目
13.a,b是任意实数,且a>b,则下列结论正确的是( )
| A. | a2>b2 | B. | $\frac{b}{a}$<1 | C. | lg(a-b)>lg$\frac{1}{a-b}$ | D. | 4-a<4-b |
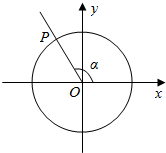 如图,已知角α的终边在第二象限,且与单位圆交于点P(m,$\frac{\sqrt{15}}{4}$).
如图,已知角α的终边在第二象限,且与单位圆交于点P(m,$\frac{\sqrt{15}}{4}$).