Question

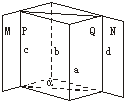
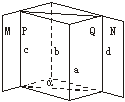
证明：如果一条直线和两个相交平面都平行，那么这条直线与这两个平面的交线平行.

 

Answer 1

答案：
解析：

解：先写出已知和求证，然后再去证明. 已知直线a∥平面M，直线a∥平面N，平面M∩平面N=b，求证：a∥b. 证法一：过直线a任意作两个平面P、Q，与平面M和N分别交于直线c，d. ∵直线a∥平面M，直线a∥平面N，∴a∥c，a∥d，∴c∥d. ∵c面N，d面N，∴c∥面N. ∵c面M，平面M∩平面N=b，∴c∥b. 又∵a∥c，∴a∥b. 证法二：在平面M∩平面N的交线b上任取一点A，则Aa， ∴点A与直线a可确定平面β. 设平面β∩平面N=b1，平面β∩平面M=b2. ∵直线a∥平面M，直线a∥平面N， ∴a∥b1，a∥b2，∴b1∥b2，则b1与b2重合，∴a∥b. 证法三：在直线a上任意取一点B，过点B作BC⊥面M，垂足为C， 由a与BC相交确定平面P，设平面P∩平面M=c， ∵直线a∥平面M，∴a∥c. ∵BC⊥面M，∴BC⊥c，∴a⊥BC. 同样可作BD⊥面N.同理a⊥BD，∴a⊥平面BCD. ∵BC⊥b，BD⊥b，∴b⊥平面BCD. ∴a∥b.