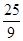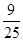题目内容
在△ABC中,角A,B,C所对边的长分别为a,b,c,若a=2,∠B=60°,b=
,则c=______,△ABC的面积是______.
| 7 |
∵a=2,cosB=cos60°,b=
,
∴由余弦定理得:b2=a2+c2-2ac•cosB,即7=4+c2-2c,
解得:c=3或c=-1(舍去),
则c=3;
∵a=2,c=3,sinB=
,
∴S△ABC=
ac•sinB=
.
故答案为:3;
| 7 |
∴由余弦定理得:b2=a2+c2-2ac•cosB,即7=4+c2-2c,
解得:c=3或c=-1(舍去),
则c=3;
∵a=2,c=3,sinB=
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
3
| ||
| 2 |
故答案为:3;
3
| ||
| 2 |

练习册系列答案
相关题目
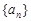 的前
的前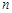 项和为
项和为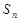 ,且
,且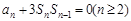 ,
,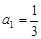 .
.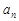 ;
;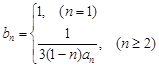 ,设
,设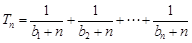 ,若
,若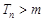 对
对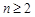 恒成立,求实数
恒成立,求实数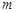 的取值范围.
的取值范围.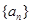 的前n项和为
的前n项和为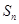 ,若
,若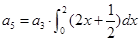 ,则
,则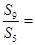 ( ).
( ).