题目内容
8.不等式2x(3-x)≥0的解集是( )| A. | (-∞,-2]∪[3,+∞) | B. | [2,3] | C. | (-∞,0]∪[3,+∞) | D. | [0,3] |
分析 直接利用二次不等式的解法求解即可.
解答 解:不等式2x(3-x)≥0对应方程的根为:0,3;
可得表达式的解集为:[0,3].
故选:D.
点评 本题考查二次不等式的解法,考查计算能力.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
17.设一直线上三点A,B,P满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$(λ≠-1),O是平面内任意一点,则用$\overrightarrow{OA}$,$\overrightarrow{OB}$表示$\overrightarrow{OP}$式子为( )
| A. | $\overrightarrow{OP}$=$\overrightarrow{OA}$+λ$\overrightarrow{OB}$ | B. | $\overrightarrow{OP}$=λ$\overrightarrow{OA}$+(1-λ)$\overrightarrow{OB}$ | ||
| C. | $\overrightarrow{OP}$=$\frac{1}{λ}$$\overrightarrow{OA}$+$\frac{1}{1+λ}$$\overrightarrow{OB}$ | D. | $\overrightarrow{OP}$=$\frac{1}{1+λ}$$\overrightarrow{OA}$+$\frac{λ}{1+λ}$$\overrightarrow{OB}$ |
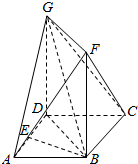 如图,在菱形ABCD中,∠DAB=60°,E为AD的中点,正方形DBFG所在平面与平面ABCD垂直.
如图,在菱形ABCD中,∠DAB=60°,E为AD的中点,正方形DBFG所在平面与平面ABCD垂直.