题目内容
a，b为异面直线，且a，b所成角为40°，直线c与a，b均异面，且所成角均为70°，则这样的c共有
3
3
条．分析：先将异面直线a，b平移到点P，结合图形可知，再分直线在面BPE的射影为∠DPE的角平分线、直线在面EPD的射影为∠BPE的角平分线时两种情况，分别进行研究，从而得出结论．
解答：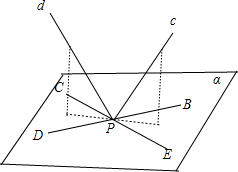
解：如图所示：先将异面直线a，b平移到点P，
BD∥a，CE∥，b，
则由题意可得∠BPE=40°、∠EPD=140°，
而∠BPE的角平分线与a和b的所成角为20°，
∠DPE的角平分线与a和b的所成角为70°，
故直线c可以是∠DPE的角平分线．
∵70°＞20°，故与a、b所成的角相等且等于70°
有且只有3条，
另外2条直线c满足直线c在面EPD的射影为∠BPE的角平分线，
即图中直线c、d，
故答案为 3．
解：如图所示：先将异面直线a，b平移到点P，BD∥a，CE∥，b，
则由题意可得∠BPE=40°、∠EPD=140°，
而∠BPE的角平分线与a和b的所成角为20°，
∠DPE的角平分线与a和b的所成角为70°，
故直线c可以是∠DPE的角平分线．
∵70°＞20°，故与a、b所成的角相等且等于70°
有且只有3条，
另外2条直线c满足直线c在面EPD的射影为∠BPE的角平分线，
即图中直线c、d，
故答案为 3．
点评：本小题主要考查异面直线所成的角、异面直线所成的角的求法，以及射影等知识，考查空间想象能力、运算能力和推理论证能力，考查转化思想，属于中档题．
练习册系列答案
相关题目