题目内容
a，b为异面直线，且a?α，b?β，若α∩β=l，则直线l必定（ ）
分析：利用异面直线、共面直线（相交和平行）的位置关系及其反证法即可得出．
解答：解：如图所示：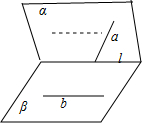
则直线l必定至少与a，b之一相交．
下面用反证法证明：如若不然，即直线l与直线a，b都不相交，因为a与l都在平面α内，
∴l∥a，同理l∥b，于是a∥b，这与已知a，b为异面直线相矛盾，因此假设不成立，则原结论成立．
故选C．
则直线l必定至少与a，b之一相交．
下面用反证法证明：如若不然，即直线l与直线a，b都不相交，因为a与l都在平面α内，
∴l∥a，同理l∥b，于是a∥b，这与已知a，b为异面直线相矛盾，因此假设不成立，则原结论成立．
故选C．
点评：熟练掌握异面直线、共面直线（相交和平行）的位置关系及其反证法是解题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目