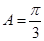题目内容
“ ”是“直线
”是“直线 与圆
与圆 相交”的
相交”的
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
A
解析试题分析:计算(0,0)到直线 的距离,d=
的距离,d=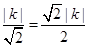 ,当k=1时,d<1,直线与圆相交;反之,若直线与圆相交,则
,当k=1时,d<1,直线与圆相交;反之,若直线与圆相交,则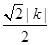 <1,解得-
<1,解得-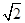 <k<
<k<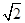 ,因此,“
,因此,“ ”是“直线
”是“直线 与圆
与圆 相交”的充分而不必要条件,故选A。
相交”的充分而不必要条件,故选A。
考点:本题主要考查充要条件的概念,直线与圆的位置关系。
点评:基础题,充要条件的判定问题,涉及知识面较广,往往是高考的热点题目。研究直线与圆的位置关系,可有两种方法,一是几何法,二是代数法。

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
下列说法错误的是( )
A.命题“若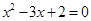 ,则 ,则 ”的逆否命题为:“若 ”的逆否命题为:“若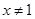 ,则 ,则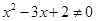 ” ” |
B.“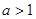 ”是“ ”是“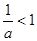 ”的充分不必要条件 ”的充分不必要条件 |
C.若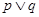 为真命题,则 为真命题,则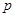 、 、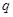 均为真命题 均为真命题 |
D.若命题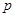 :“存在 :“存在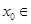 R, R,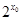 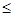 0”,则 0”,则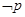 :“对任意的 :“对任意的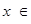 R, R,  >0”. >0”. |
若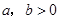 ,则
,则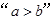 是“
是“ ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分且必要条件 | D.既非充分也非必要条件 |
下列命题中,真命题是
A. | B. |
C. | D. |
已知命题 ,则
,则 是 ( )
是 ( )
A. | B.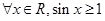 |
C.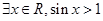 | D.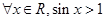 |
已知q是等比数列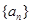 的公比,则“
的公比,则“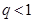 ”是“数列
”是“数列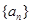 是递减数列”的( )
是递减数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 ∶
∶ ,
, ∶
∶ ,则
,则 是
是 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
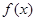 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,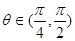 ,则
,则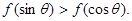
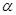 、
、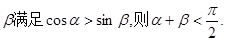
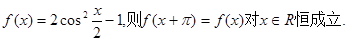
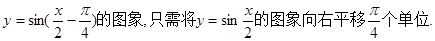
 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,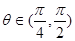 ,
,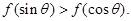
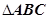 中,
中,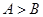 是
是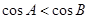 的充要条件.
的充要条件. 为非零向量,且
为非零向量,且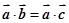 ,则
,则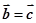 .
.