题目内容
已知函数 。
。
(1)若不等式 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(2)设 ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数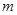 的取值范围。
的取值范围。
(1)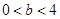 ;(2)
;(2)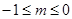 或
或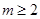 。
。
解析试题分析:解(1) 对任意的实数
对任意的实数 恒成立,即
恒成立,即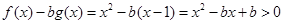 恒成立,即
恒成立,即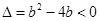 --------3分
--------3分
所以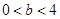 -----------1分
-----------1分
(2)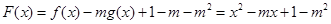 ,
,
其中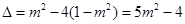
①当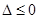 ,即
,即 时,则
时,则 ,得
,得 。--2分
。--2分
②当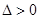 ,即
,即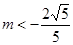 或
或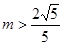 时,设方程
时,设方程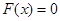 的根为
的根为 。
。
若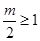 ,则
,则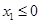 ,则
,则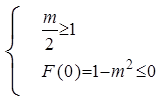 ,得
,得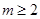 ;-----3分
;-----3分
若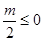 ,则
,则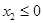 ,则
,则 ,得
,得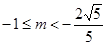 。--3分
。--3分
综上,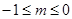 或
或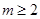 ------------------------1分
------------------------1分
考点:二次函数的性质;函数图像的对称变换;二次方程根的分布问题。
点评:(1)若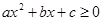
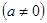 恒成立
恒成立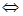
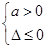 ;若
;若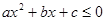
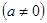 恒成立
恒成立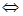
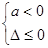 。若题中没有限制二次项系数不为零,就需要讨论二次项系数是否为0。
。若题中没有限制二次项系数不为零,就需要讨论二次项系数是否为0。

练习册系列答案
相关题目
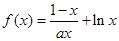
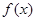 在
在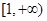 上为增函数,求正实数
上为增函数,求正实数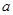 的取值范围;
的取值范围;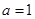 时,求
时,求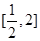 上的最大值和最小值;
上的最大值和最小值;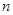 ,都有
,都有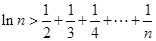 。
。 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数 的最小值;
的最小值; 的函数
的函数 是奇函数.
是奇函数. 的值;
的值; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 上是增函数还是减函数?并用定义证明.
上是增函数还是减函数?并用定义证明.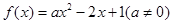 .
.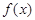 有两个零点,求
有两个零点,求 的取值范围;
的取值范围;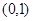 与
与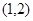 上各有一个零点,求
上各有一个零点,求 (
(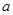 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数 是区间[-1,1]上的减函数
是区间[-1,1]上的减函数 的取值范围;
的取值范围; 在
在 上恒成立,求
上恒成立,求 的取值范围。
的取值范围。 的定义域.
的定义域.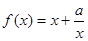 定义域为
定义域为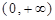 ,且
,且 .
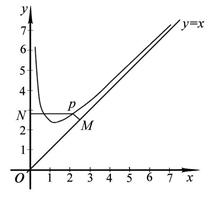
.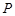 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点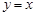 和
和 轴的垂线,垂足分别为
轴的垂线,垂足分别为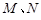 .
.
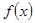 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分)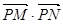 是否为定值?若是,则求出该定值,若不是,则说明理由;(7分)
是否为定值?若是,则求出该定值,若不是,则说明理由;(7分) 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.(7分)
面积的最小值.(7分)