题目内容
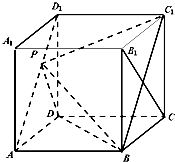 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P为线段AD1上的点,且满足| D1P |
| PA |
(Ⅰ)当λ=1时,求证:平面ABC1D1⊥平面PDB;
(Ⅱ)试证无论λ为何值,三棱锥D-PBC1的体积恒为定值.
分析:(I)欲证平面ABC1D1⊥平面PDB,根据面面垂直的判定定理可知在平面PDB内一直线与平面ABC1D1垂直,根据面面垂直的性质定理可知DP⊥平面ABC1D1;
(II)根据AD1∥BC1,P为线段AD1上的点,得到三角形PBC1的面积为定值,再根据CD∥平面ABC1D1,得到点D到平面PBC1的距离为定值,从而得到三棱锥D-BPC1的体积为定值,在利用体积公式求出三棱锥D-PBC1的体积即可.
(II)根据AD1∥BC1,P为线段AD1上的点,得到三角形PBC1的面积为定值,再根据CD∥平面ABC1D1,得到点D到平面PBC1的距离为定值,从而得到三棱锥D-BPC1的体积为定值,在利用体积公式求出三棱锥D-PBC1的体积即可.
解答: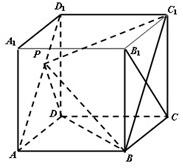 证明:(Ⅰ)∵正方体ABCD-A1B1C1D1中,AB⊥面AA1D1D,
证明:(Ⅰ)∵正方体ABCD-A1B1C1D1中,AB⊥面AA1D1D,
又AB?ABC1D1∴平面ABC1D1⊥平面AA1D1D,
∵λ=1时,P为AD1的中点,∴DP⊥AD1,
又∵平面ABC1D1∩平面AA1D1D=AD1,
∴DP⊥平面ABC1D1,
又DP?平面PDB,∴平面ABC1D1⊥平面PDB.
(Ⅱ)∵AD1∥BC1,P为线段AD1上的点,
∴三角形PBC1的面积为定值,
即S△PBC1=
×
×1=
,
又∵CD∥平面ABC1D1,
∴点D到平面PBC1的距离为定值,即h=
,
∴三棱锥D-BPC1的体积为定值,
即VD-PBC1=
•S△PBC1•h=
×
×
=
.
也即无论λ为何值,三棱锥D-PBC1的体积恒为定值
.
 证明:(Ⅰ)∵正方体ABCD-A1B1C1D1中,AB⊥面AA1D1D,
证明:(Ⅰ)∵正方体ABCD-A1B1C1D1中,AB⊥面AA1D1D,又AB?ABC1D1∴平面ABC1D1⊥平面AA1D1D,
∵λ=1时,P为AD1的中点,∴DP⊥AD1,
又∵平面ABC1D1∩平面AA1D1D=AD1,
∴DP⊥平面ABC1D1,
又DP?平面PDB,∴平面ABC1D1⊥平面PDB.
(Ⅱ)∵AD1∥BC1,P为线段AD1上的点,
∴三角形PBC1的面积为定值,
即S△PBC1=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
又∵CD∥平面ABC1D1,
∴点D到平面PBC1的距离为定值,即h=
| ||
| 2 |
∴三棱锥D-BPC1的体积为定值,
即VD-PBC1=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 6 |
也即无论λ为何值,三棱锥D-PBC1的体积恒为定值
| 1 |
| 6 |
点评:本小题主要考查平面与平面垂直的判定,以及棱锥的体积等有关知识,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于基础题.

练习册系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
