题目内容
11. 四棱锥P-ABCD的底面ABCD是平行四边形,PA=AD,M,N分别是棱PC,AB的中点,且MN⊥CD.
四棱锥P-ABCD的底面ABCD是平行四边形,PA=AD,M,N分别是棱PC,AB的中点,且MN⊥CD.(Ⅰ)求证:PN=CN;
(Ⅱ)直线MN与平面PBD相交于点F,求MF:FN.
分析 (Ⅰ)取PD中点E,连AE,EM,证明MN⊥平面PCD,可得MN⊥PC,即可证明PN=CN;
(Ⅱ)设M,N,C,A到平面PBD的距离分别为d1,d2,d3,d4,则d3=2d1,d4=2d2,由VA-PBD=VC-PBD,得d3=d4,则d1=d2,即可得出结论.
解答  (Ⅰ)证明:取PD中点E,连AE,EM,
(Ⅰ)证明:取PD中点E,连AE,EM,
则EM∥AN,且EM=AN,
四边形ANME是平行四边形,MN∥AE.
由PA=AD得AE⊥PD,故MN⊥PD.
又因为MN⊥CD,所以MN⊥平面PCD,
则MN⊥PC,PN=CN.…(6分)
(Ⅱ)解:设M,N,C,A到平面PBD的距离分别为d1,d2,d3,d4,则d3=2d1,d4=2d2,
由VA-PBD=VC-PBD,得d3=d4,则d1=d2,
故MF:FN=d1:d2=1:1.…(12分)
点评 本题考查线面垂直的证明,考查等体积的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.已知集合A={1,2,3},B={Z∈Z|1<x<4},则A∩B=( )
| A. | {1} | B. | {2,4} | C. | {2,3} | D. | (1,4) |
20.某市修建经济适用房,已知A、B、C三个社区分别有低收入家庭400户、300户、200户,若首批经济适用房有90套住房用于解决住房紧张问题,采用分层抽样的方法决定各社区户数,则应从A社区中抽取低收入家庭的户数为( )
| A. | 40 | B. | 36 | C. | 30 | D. | 20 |
1.执行如图所示的算法流程图.若输入x=0,则输出的y的值是( )
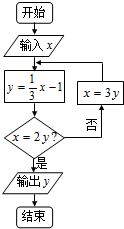

| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
 某校为了调查“学业水平考试”学生的数学成绩,随机地抽取该校甲、乙两班各10名同学,获得的数据如下:(单位:分)
某校为了调查“学业水平考试”学生的数学成绩,随机地抽取该校甲、乙两班各10名同学,获得的数据如下:(单位:分) 某校在2014年对2000名高一新生进行英语特长测试选拔,现抽取部分学生的英语成绩,将所得数据整理后得出频率分布直方图如图所示,图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
某校在2014年对2000名高一新生进行英语特长测试选拔,现抽取部分学生的英语成绩,将所得数据整理后得出频率分布直方图如图所示,图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.