题目内容
连接椭圆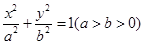
的一个焦点和一个顶点得到的直线方程为
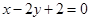，则该椭圆的离心率为（ ）
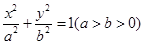的一个焦点和一个顶点得到的直线方程为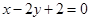，则该椭圆的离心率为（ ）A． | B． | C． | D． |
A
直线
与x轴交点为（-2,0），与y轴交点为（0,1）；根据题意知
故选A
与x轴交点为（-2,0），与y轴交点为（0,1）；根据题意知故选A
练习册系列答案
阅读快车系列答案
相关题目
题目内容
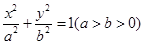的一个焦点和一个顶点得到的直线方程为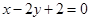，则该椭圆的离心率为（ ）| A． | B． | C． | D． |
与x轴交点为（-2,0），与y轴交点为（0,1）；根据题意知故选A阅读快车系列答案
的离心率为
，直线
过点
，
，且与椭圆
相切于点
.
与椭圆
、
，使得
?若存在，试求出直线
,离心率
.
与椭圆交于不同的两点
，且线段
的中点的横坐标为
，求直线
且与椭圆
有相同焦点的椭圆方程。
的两个顶点
为椭圆的两个焦点，其余四个顶点在
的离心率为
分别是左、右焦点，过F1的直线与圆
相切，且与椭圆E交于A、B两点。
时，求椭圆E的方程；
的离心率是
，则双曲线
=1的离心率是______。
是椭圆的两焦点，
为椭圆上一点，若
，则离心率
的范围是___________.
)和(0，－
，求此椭圆方程．