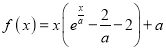题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 和
和![]() 两点.
两点.
(1)当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)若过点![]() 且垂直于直线
且垂直于直线![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,记
两点,记![]() 与
与![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)12.
;(2)12.
【解析】
(1) 设直线方程为![]() ,联立直线与抛物线的方程,利用韦达定理求解得
,联立直线与抛物线的方程,利用韦达定理求解得![]() 即可.
即可.
(2) 联立直线与抛物线的方程,利用韦达定理表达![]() ,再根据基本不等式的方法求最小值即可.
,再根据基本不等式的方法求最小值即可.
解: (1)由直线![]() 过定点
过定点![]() ,可设直线方程为
,可设直线方程为![]() .
.
联立![]() 消去
消去![]() ,得
,得![]() ,
,
由韦达定理得![]() ,
,
所以![]() .
.
因为![]() .所以
.所以![]() ,解得
,解得![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
(2)由(1),知![]() 的面积为
的面积为![]()
![]() .
.
因为直线![]() 与直线
与直线![]() 垂直,
垂直,
且当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,则此时直线
,则此时直线![]() 的方程为
的方程为![]() ,
,
但此时直线![]() 与抛物线
与抛物线![]() 没有两个交点,
没有两个交点,
所以不符合题意,所以![]() .因此,直线
.因此,直线![]() 的方程为
的方程为![]() .
.
同理,![]() 的面积
的面积![]() .
.
所以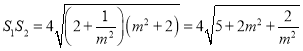
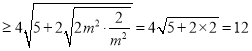 ,
,
当且仅当![]() ,即
,即![]() ,亦即
,亦即![]() 时等号成立.
时等号成立.

练习册系列答案
相关题目
【题目】下表给出的是某城市![]() 年至
年至![]() 年,人均存款
年,人均存款![]() (万元),人均消费
(万元),人均消费![]() (万元)的几组对照数据.
(万元)的几组对照数据.
年份 |
|
|
|
|
人均存款 |
|
|
|
|
人均消费 |
|
|
|
|
(1)试建立![]() 关于
关于![]() 的线性回归方程;如果该城市
的线性回归方程;如果该城市![]() 年的人均存款为
年的人均存款为![]() 万元,请根据线性回归方程预测
万元,请根据线性回归方程预测![]() 年该城市的人均消费;
年该城市的人均消费;
(2)计算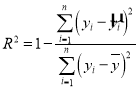 ,并说明线性回归方程的拟合效果.
,并说明线性回归方程的拟合效果.
附:回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为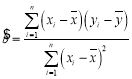 ,
,![]() .
.