题目内容
设函数![]()
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)如果对任何![]() ,都有
,都有![]()
![]() ,求
,求![]() 的取值范围。
的取值范围。
解:(Ⅰ)![]()
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() 。
。
因此![]() 在每一个区间
在每一个区间![]() 是增函数,
是增函数,
![]() 在每一个区间
在每一个区间![]() 是减函数。
是减函数。
(Ⅱ)令![]() ,则
,则
![]()
![]()
![]()
故当![]() 时,
时,![]() ,又
,又![]() ,所以当
,所以当![]() 时,
时,![]() =0,即
=0,即
![]()
当![]() 时,令
时,令![]() ,则
,则![]()
故当![]() 时,
时,![]() ,因此
,因此![]() 在
在![]() 上单调增加
上单调增加
故当![]() 时,
时,![]() ,即
,即
![]()
于是,当![]() 时
时
![]()
当![]() 时,有
时,有![]()
因此,![]() 的取值范围是
的取值范围是![]() 。
。

练习册系列答案
相关题目
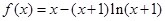 (
(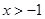 ).
).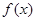 的单调区间;
的单调区间;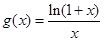 (
(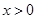 )的单调性证明:当
)的单调性证明:当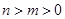 时,
时, ;
;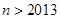 ,且
,且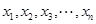 均为正实数,
均为正实数, 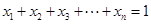 时,
时,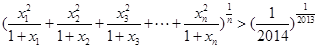 .
. .
.